/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 18 kwietnia 2015 Czas pracy: 90 minut
Informacja do zadań 1 i 2
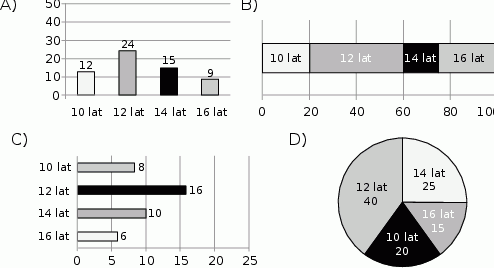
W tabeli przedstawiono procentowy podział uczestników obozu ze względu na wiek.
| Wiek uczestnika | Liczba uczestników |
| 10 lat | 20% |
| 12 lat | 40% |
| 14 lat | 25% |
| 16 lat | 15% |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Średnia wieku uczestników obozu jest równa
A) 12 lat B) 12,7 lat C) 13 lat D) 14 lat
Który z diagramów nie może przedstawiać informacji dotyczących wieku uczestników obozu? Wybierz odpowiedź spośród podanych.
W pewnej fabryce są dwie linie produkcyjne produkujące identyczne układy elektroniczne. Obydwie linie produkcyjne wytwarzają łącznie 720 układów w ciągu 8 godzin, a sama druga linia produkcyjna wytwarza 558 układów w ciągu 12 godzin.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwsza linia produkcyjna pracuje z mniejszą wydajnością niż druga. | P | F |
| Pierwsza linia produkcyjna w ciągu 8 godzin wykonuje 352 układy. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odległość dwóch liczb na osi liczbowej jest równa 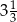 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 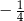 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa
A) 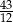 B)
B) 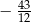 C)
C) 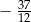 D)
D) 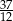
Dane są liczby: 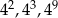 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Iloczyn tych liczb jest równy
A) 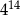 B)
B) 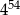 C)
C) 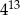 D)
D) 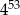
Która z liczb nie spełnia warunku 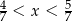 ?
?
Wybierz odpowiedź spośród podanych.
A) 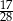 B)
B) 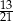 C)
C) 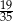 D)
D) 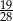
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Cenę płyty kompaktowej obiżono najpierw o 10%, a potem o 20%. Cena płyty po tych dwóch obniżkach wynosi 72 zł. Cena tej płyty przed obniżkami była równa
A) 93,6 zł. B) 100 zł. C) 96 zł. D) 108 zł.
Dane są rozwinięcia dziesiętne okresowe dwóch liczb
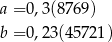
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na  –tym miejscu po przecinku w obu rozwinięciach znajduje się ta sama cyfra dla
–tym miejscu po przecinku w obu rozwinięciach znajduje się ta sama cyfra dla
A) 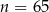 B)
B) 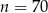 C)
C) 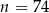 D)
D) 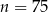
Zając porusza się z prędkością 40 km/h wykonując skoki długości 80 cm.
Ile skoków wykona zając w czasie 9 minut? Wybierz odpowiedź spośród podanych.
A) 1000 skoków B) 7500 skoków C) 6400 skoków D) 2000 skoków
Informacja do zadań 10 i 11
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
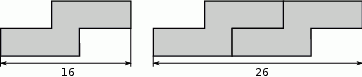
Ułożono wzór z 4 płytek, jak na rysunku.
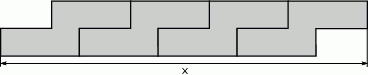
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odcinek  ma długość
ma długość
A) 46 cm B) 64 cm C) 36 cm D) 52 cm
Które wyrażenie algebraiczne opisuje długość analogicznego do  odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek? Wybierz odpowiedź spośród podanych.
płytek? Wybierz odpowiedź spośród podanych.
A) 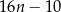 B)
B) 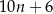 C)
C) 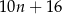 D)
D) 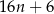
Samochód przebył trasę łączącą miejscowości 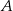 i
i 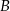 ze średnią prędkością
ze średnią prędkością 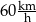 , a potem pokonał trasę między miejscowościami
, a potem pokonał trasę między miejscowościami 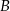 i
i 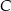 ze średnią prędkością
ze średnią prędkością 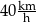 . Odległość między miastami
. Odległość między miastami 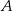 i
i 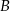 jest taka sama jak odległość między miastami
jest taka sama jak odległość między miastami 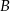 i
i 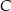 i wynosi 120 km.
i wynosi 120 km.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Średnia prędkość z jaką samochód przejechał całą trasę między 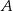 i i 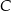 jest równa jest równa 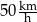 . . | P | F |
Gdyby średnia prędkość samochodu na trasie pomiędzy miastami 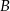 i i 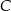 była równa była równa 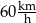 , to samochód pokonałby całą trasę między miastami , to samochód pokonałby całą trasę między miastami 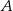 i i 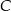 w czasie o godzinę krótszym. w czasie o godzinę krótszym. | P | F |
Piechur szedł z punktu 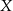 do punktu
do punktu 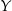 ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu
ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu 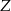 .
.
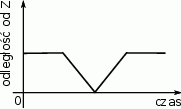
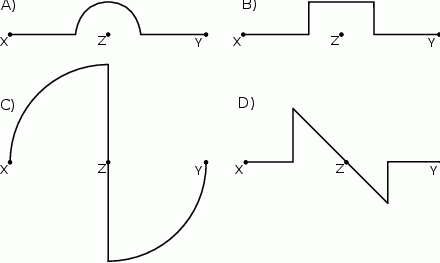
Na którym z poniższych rysunków zilustrowano, jak mogła wyglądać trasa piechura pomiędzy punktami 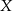 i
i 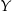 ? Wybierz odpowiedź spośród podanych.
? Wybierz odpowiedź spośród podanych.
Kształt i wymiary deski do krojenia przedstawiono na rysunku.
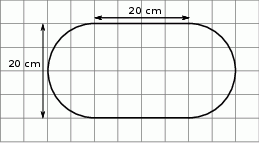
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Powierzchnia tej deski (w 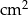 ) jest równa
) jest równa
A) 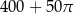 B)
B) 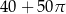 C)
C) 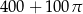 D)
D) 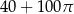
Rzucamy jeden raz sześcienną kostką do gry. Oznaczmy przez 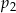 prawdopodobieństwo wyrzucenia liczby parzystej, a przez
prawdopodobieństwo wyrzucenia liczby parzystej, a przez 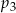 – prawdopodobieństwo wyrzucenia liczby większej od 3.
– prawdopodobieństwo wyrzucenia liczby większej od 3.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 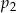 jest większa od liczby jest większa od liczby 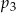 . . | P | F |
Liczby 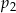 i i 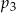 są większe od są większe od 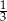 | P | F |
Na rysunku przedstawiono romb i jego przekątne. Długości odcinków na jakie dzielą się przekątne tego rombu są opisane za pomocą wyrażeń.
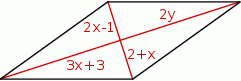
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód rombu jest równy 52. | P | F |
| Pole rombu jest równe 240. | P | F |
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 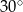 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Na rysunku przedstawiono graniastosłup prosty i jego wymiary.
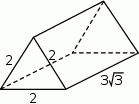
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Objętość tego graniastosłupa jest równa
A)  B) 9 C)
B) 9 C) 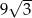 D)
D) 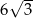
Na rysunku przedstawiono dwa prostokąty.

Czy te prostokąty te są figurami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa prostokąty są podobne. |
| B) | długości boków jednego prostokąta nie są proporcjonalne do długości boków drugiego prostokąta. |
| C) | długości boków jednego prostokąta są proporcjonalne do długości boków drugiego prostokąta. |
Dane są: kula o promieniu  , walec o promieniu podstawy
, walec o promieniu podstawy  i wysokości
i wysokości  , oraz stożek o promieniu podstawy
, oraz stożek o promieniu podstawy  i tworzącej długości
i tworzącej długości 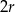 .
.
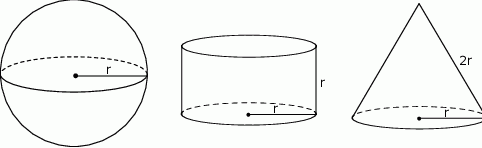
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole powierzchni całkowitej stożka jest równe polu powierzchni kuli. | P | F |
| Pole powierzchni całkowitej walca jest równe polu powierzchni kuli. | P | F |
Olaf, Marysia i Kamil przygotowują farbę do pomalowania swoich pokojów. Każde z nich potrzebuje 12 litrów farby i każde z nich miesza ze sobą dwa rodzaje farby: białą, która jest dostępna w większych puszkach i granatową, która jest dostępna w mniejszych puszkach. Olaf przygotował 12 litrów farby mieszając farbę z 6 dużych puszek i 4 małych, a Marysia przygotowała tę samą ilość farby mieszając farbę z 5 dużych i 6 małych puszek. Kamil chce przygotować swoją farbę używając 7 dużych puszek i jednej małej. Czy wystarczy mu farby do pomalowania pokoju? Uzasadnij odpowiedź.

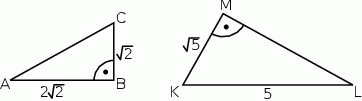
Uzasadnij, że trójkąty prostokątne 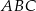 i
i 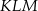 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.
Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe 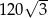 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 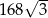 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.

