/Gimnazjum/Egzamin gimnazjalny
Egzamin Gimnazjalny
z Matematyki 24 kwietnia 2013 Czas pracy: 90 minut
Informacja do zadań 1 i 2
W tabeli przedstawiono informacje dotyczące wieku wszystkich uczestników obozu narciarskiego.
| Wiek uczestnika | Liczba uczestników |
| 10 lat | 5 |
| 14 lat | 3 |
| 15 lat | 4 |
| 16 lat | 8 |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Mediana wieku uczestników obozu jest równa
A) 14 lat B) 14,5 roku C) 15 lat D) 15,5 roku
Na którym diagramie poprawnie przedstawiono procentowy podział uczestników obozu ze względu na wiek? Wybierz odpowiedź spośród podanych.
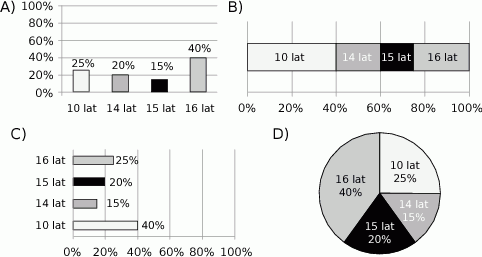
W pewnej hurtowni za 120 jednakowych paczek herbaty trzeba zapłacić 1500 zł.
Ile takich paczek herbaty można kupić w tej hurtowni za 600 zł, przy tej samej cenie za jedną paczkę? Wybierz odpowiedź spośród podanych.
A) 48 B) 50 C) 52 D) 56
Cena brutto = cena netto + podatek VAT
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto 1 kg jabłek jest równa 2,50 zł, a cena brutto jest równa 2,70 zł, to podatek VAT wynosi 8% ceny netto. | P | F |
| Jeżeli cena netto podręcznika do matematyki jest równa 22 zł, to cena tej książki z 5% podatkiem VAT wynosi 24,10 zł. | P | F |
Ile spośród liczb: 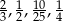 spełnia warunek
spełnia warunek 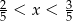 ?
?
Wybierz odpowiedź spośród podanych.
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
Dane są liczby 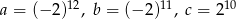 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczby te uporządkowane od najmniejszej do największej to:
A) 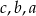 B)
B) 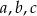 C)
C) 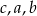 D)
D) 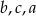
Dane są liczby  i
i 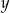 spełniające warunki:
spełniające warunki: 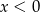 i
i 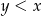 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 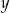 jest ujemna. jest ujemna. | P | F |
Liczba  jest większa od liczby jest większa od liczby 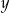 . . | P | F |
Informacja do zadań 8 i 9
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w 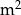 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika.
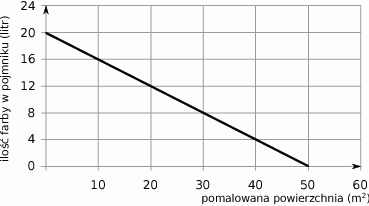
Ile farby pozostało w pojemniku po pomalowaniu 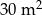 ściany? Wybierz odpowiedź spośród podanych.
ściany? Wybierz odpowiedź spośród podanych.
A) 8 litrów B) 12 litrów C) 16 litrów D) 20 litrów
Ile farby zużyto na pomalowanie 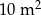 ściany? Wybierz odpowiedź spośród podanych.
ściany? Wybierz odpowiedź spośród podanych.
A) 4 litry B) 8 litrów C) 10 litrów D) 16 litrów
W pudełku było 20 kul białych i 10 czarnych. Dołożono jeszcze 10 kul białych i 15 czarnych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
Średnia prędkość samochodu na trasie przebytej w czasie 4 godzin wyniosła 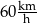 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Aby czas przejazdu był o 1 godzinę krótszy, średnia prędkość samochodu na tej trasie musiałaby wynosić 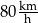 . . | P | F |
Gdyby średnia prędkość samochodu na tej trasie była równa 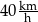 , to czas przejazdu byłby równy 6 godzin. , to czas przejazdu byłby równy 6 godzin. | P | F |
Ania ma w skarbonce 99 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy więcej niż pięciozłotowych.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 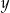 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 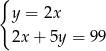 B)
B) 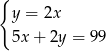 C)
C) 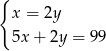 D)
D) 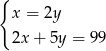
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga  jego wysokości.
jego wysokości.
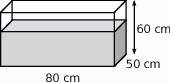
Ile litrów wody jest w akwarium?
Wybierz odpowiedź spośród podanych.
A) 16000 litrów B) 1600 litrów C) 160 litrów D) 16 litrów
W równoległoboku 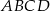 bok
bok 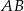 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 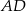 . Punkt
. Punkt 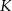 jest środkiem boku
jest środkiem boku 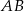 , a punkt
, a punkt 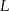 jest środkiem boku
jest środkiem boku 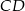 .
.
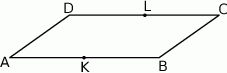
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 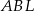 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 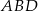 . . | P | F |
Pole równoległoboku 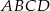 jest cztery razy większe od pola trójkąta jest cztery razy większe od pola trójkąta 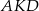 . . | P | F |
Punkt 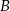 jest środkiem okręgu. Prosta
jest środkiem okręgu. Prosta 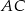 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 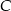 ,
, 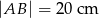 i
i 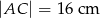 .
.
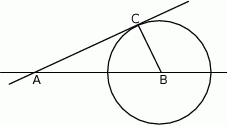
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Promień 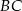 okręgu ma długość
okręgu ma długość
A) 12 cm B) 10 cm C) 4 cm D) 2 cm
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 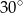 większą niż kąt
większą niż kąt  , a trzeci ma miarę trzy razy większą niż kąt
, a trzeci ma miarę trzy razy większą niż kąt  .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
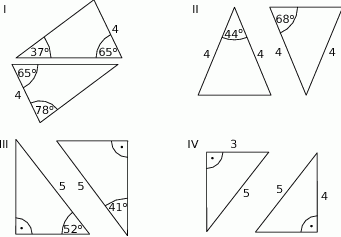
Na którym rysunku trójkąty nie są przystające? Wybierz odpowiedź spośród podanych.
A) I B) II C) III D) IV
Kąt ostry rombu ma miarę 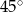 , a wysokość rombu jest równa
, a wysokość rombu jest równa 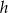 .
.
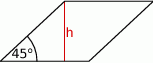
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole tego rombu można wyrazić wzorem
A) 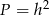 B)
B) 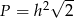 C)
C) 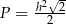 D)
D) 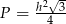
Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
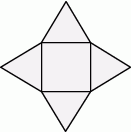
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wszystkie krawędzie tego ostrosłupa mają taką samą długość. | P | F |
| Wysokość tego ostrosłupa jest mniejsza niż wysokość jego ściany bocznej. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Suma objętości 8 kul, z których każda ma promień 1, jest taka sama jak objętość jednej kuli o promieniu
A) 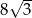 B) 8 C)
B) 8 C) 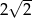 D) 2
D) 2
W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
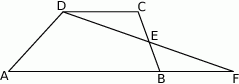
Na rysunku przedstawiono trapez 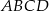 i trójkąt
i trójkąt 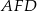 . Punkt
. Punkt 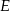 leży w połowie odcinka
leży w połowie odcinka 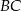 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 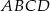 i pole trójkąta
i pole trójkąta 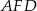 są równe.
są równe.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 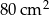 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 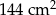 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.

