/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 23 marca 2013 Czas pracy: 90 minut
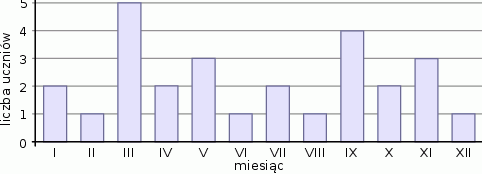
Na diagramie zaznaczono, w których miesiącach urodzili się uczniowie klasy IIa.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że
A) klasa IIa liczy 28 uczniów.
B) najwięcej uczniów urodziło się w kwietniu.
C) większość uczniów urodziła się w pierwszej połowie roku.
D) liczba uczniów urodzonych w maju jest większa niż łączna liczba uczniów urodzonych w lipcu i w sierpniu.
Po usunięciu z zestawu liczb: 15, 10, 4, 5, 9, 12, 8 jednej liczby średnia liczb nie zmieniła się.
Którą z poniższych liczb usunięto? Wybierz odpowiedź spośród podanych.
A) 8 B) 9 C) 10 D) 12
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Co trzeci uczeń biorący udział w zawodach był uczniem klasy trzeciej, co czwarty był uczniem klasy piątej, a pozostałych 15 uczniów było uczniami klasy czwartej. W zawodach brało udział
A) 28 uczniów. B) 32 uczniów. C) 36 uczniów. D) 48 uczniów.
Informacja do zadań 4 i 5
W sobotę Patrycja wyruszyła z Ptasiej Doliny na górski spacer, w trakcie którego odwiedziła kolejno dwa pobliskie szczyty: Kaczą Górę i Łąbędzią Górę. Na schematycznej mapce przedstawiono drogę jaką pokonała Patrycja, a na wykresie – jak zmieniała się w trakcie spaceru jej względna wysokość (w metrach) mierzona od poziomu Ptasiej Doliny.
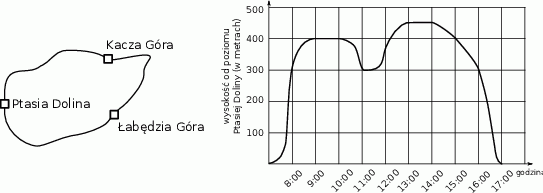
Jaka jest różnica wysokości między Łabędzią Górą, a Kaczą Górą? Wybierz odpowiedź spośród podanych.
A) 50 m B) 100 m C) 150 m D) 400 m
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na każdym ze szczytów Patrycja zrobiła godzinną przerwę. | P | F |
| Od momentu zejścia z Kaczej Góry do momentu wejścia na Łąbędzią Górę upłynęły 4 godziny. | P | F |
| Patrycja wróciła do punktu wyjścia po 9 godzinach. | P | F |
| W ciągu przedostatniej godziny spaceru Patrycja zeszła w dół o 100 metrów. | P | F |
W pudełku znajduje się 18 losów, wśród których są 2 losy wygrywające.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu przegrywającego jest dziewięciokrotnie większe, niż wyciągnięcia losu wygrywającego. | P | F |
| Jeżeli do pudełka włożymy dwa losy wygrywające to prawdopodobieństwo wygranej wzrośnie o 100%. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Cena książki po podwyżce o 20% wynosi 84 zł. Cena tej książki przed podwyżką była równa
A) 70 zł. B) 56 zł. C) 67,20 zł. D) 82,35 zł.
Samolot pasażerski spala średnio 10 ton paliwa w ciągu godziny lotu.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ciągu minuty lotu samolot spala ponad 200 kg paliwa. | P | F |
| Spalenie przez samolot 1800 kg paliwa trwa krócej niż 12 minut. | P | F |
Korzystając z tego, że 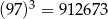 , wskaż wartość liczby
, wskaż wartość liczby 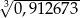 .
.
Zaznacz dobrą odpowiedź.
A) 0,0097 B) 0,097 C) 0,97 D) 9,7
Do okręgu o środku 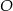 należą punkty
należą punkty 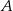 i
i 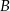 . Okrąg ma promień 48, a łuk
. Okrąg ma promień 48, a łuk 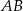 ma długość
ma długość 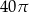 .
.
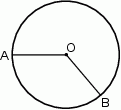
Jaką miarę ma kąt środkowy oparty na tym łuku?
Wybierz odpowiedź spośród podanych.
A) 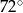 B)
B) 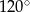 C)
C) 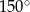 D)
D) 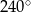
Informacja do zadań 11 – 13
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 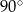 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
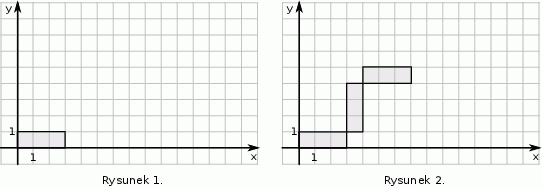
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Marcel narysował w ten sposób pięć prostokątów. Współrzędna  prawego górnego wierzchołka piątego prostokąta jest równa
prawego górnego wierzchołka piątego prostokąta jest równa
A) 11 B) 10 C) 9 D) 8
Oceń prawdziwość podanych zdań.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli punkt  jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to
 | P | F |
 | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Współrzędne prawego górnego wierzchołka 39 prostokąta są równe 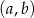 . Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
. Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
A) 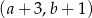 B)
B) 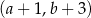 C)
C) 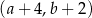 D)
D) 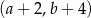
Dany jest trapez prostokątny  , w którym trójkąt
, w którym trójkąt  jest trójkątem równobocznym o boku długości 6 cm.
jest trójkątem równobocznym o boku długości 6 cm.
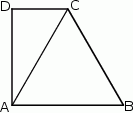
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
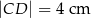 | P | F |
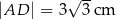 | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
W prostokącie o obwodzie 24 cm jeden bok jest dłuższy od drugiego o 4 cm. Pole tego prostokąta jest równe
A) 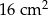 B)
B) 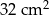 C)
C) 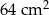 D)
D) 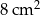
W układzie współrzędnych zaznaczono wierzchołki 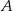 i
i 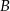 rombu
rombu 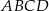 oraz jedną z jego osi symetrii.
oraz jedną z jego osi symetrii.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Pole rombu  jest równe
jest równe
A) 2 B) 4 C) 6 D) 8
Na rysunku przedstawiono dwa trójkąty prostokątne.
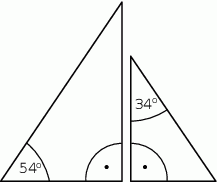
Czy te trójkąty są trójkątami podobnymi? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | każde dwa trójkąty prostokątne są podobne. |
| B) | miary kątów ostrych jednego trójkąta są różne od miar kątów ostrych drugiego trójkąta. |
| C) | miary kątów ostrych jednego trójkąta są takie same jak miary kątów ostrych drugiego trójkąta. |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli długość każdej krawędzi podstawy ostrosłupa prawidłowego czworokątnego zmniejszymy 2 razy, a jego wysokość zwiększymy 4 razy, to objętość ostrosłupa
A) zwiększy się czterokrotnie. B) zwiększy się dwukrotnie.
C) zmniejszy się dwukrotnie. D) nie zmieni się.
Z 9 sześcianów o krawędziach długości 2 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup? Wybierz odpowiedź spośród A–E.
| I | 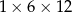 |
| II | 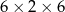 |
| III | 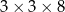 |
| IV | 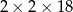 |
| V | 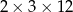 |
A) II, III i IV B) III i IV C) II i IV D) Wszystkie podane.
Do sklepu rowerowego dostarczono 30 rowerów dziecięcych, wśród których były dwa rodzaje rowerów: dwukołowe i trójkołowe. W sumie w dostarczonych rowerach było 67 kół. Ile rowerów dwukołowych i ile rowerów trójkołowych dostarczono do sklepu? Zapisz obliczenia.
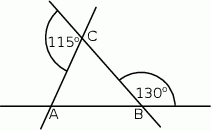
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt  . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt  jest równoramienny.
jest równoramienny.
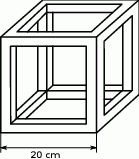
Na rysunku przedstawiono model sześcianu wykonany z listewek, których przekrój poprzeczny jest kwadratem o boku 2 cm. Krawędź sześcianu ma długość 20 cm. Oblicz jaka jest powierzchnia całkowita tego modelu. Zapisz obliczenia.