/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 16 marca 2019 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Poniższa tabela przedstawia temperaturę odczytywaną o tej samej porze w kolejnych dniach tygodnia.
| Poniedziałek | Wtorek | Środa | Czwartek | Piątek | Sobota | Niedziela |
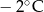 | 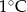 | 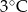 | 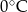 | 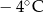 | 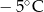 | 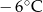 |
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Maksymalna różnica temperatur pomiędzy dwoma dniami tego tygodnia jest równa
A) 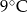 B)
B) 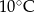 C)
C) 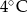 D)
D) 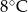
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Średnia temperatura tego tygodnia była niższa niż  . . | P | F |
| Przez cztery kolejne dni tego tygodnia temperatura malała. | P | F |
Renesansową kamienicę z 1573 roku poddano renowacji w XVIII wieku i umieszczono na niej datę tej renowacji – MDCCXLIX. Po ilu latach od wybudowania dokonano renowacji tej kamienicy? Wybierz właściwą odpowiedź spośród podanych.
A) Po 376 latach. B) Po 176 latach. C) Po 396 latach. D) Po 196 latach.
Średnie zużycie paliwa na pierwszym odcinku trasy było równe 7 litrów na 100 kilometrów, a średnie zużycie paliwa na drugim, dwa razy dłuższym odcinku trasy, było równe 10 litrów na 100 kilometrów.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Średnie zużycie paliwa na każde 100 km całej trasy wyniosło
A) 8 litrów. B) 8,5 litra. C) 7 litrów. D) 9 litrów.
W ciągu 20 dni zakład produkcyjny wykonał 2400 sztuk produktu. O ile procent należy zwiększyć wydajność produkcji, aby tę samą pracę wykonać w 16 dni?
Wybierz właściwą odpowiedź spośród podanych.
A) 20% B) 25% C) 15% D) 30%
Dane są dwie liczby: 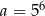 ,
, 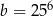 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn 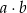 jest równy jest równy 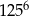 . . | P | F |
Iloraz 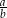 jest równy jest równy 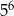 . . | P | F |
W układzie współrzędnych zaznaczono wierzchołki 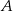 i
i  kwadratu
kwadratu  .
.
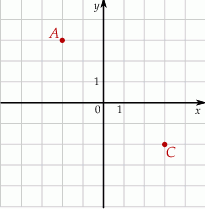
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole kwadratu  jest równe
jest równe
A) 25 B) 20 C) 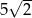 D) 5
D) 5
Uczestnicy obozu wędrownego w ciągu drugiego dnia marszu pokonali dwa razy dłuższy odcinek trasy niż w ciągu pierwszego dnia, a w ciągu trzeciego dnia marszu pokonali dystans trzy razy krótszy niż drugiego dnia. W sumie w ciągu trzech dni pokonali trasę długości 60,5 km.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Odcinek trasy, który turyści przeszli w drugim dniu wędrówki miał długość
A) 16,5 km B) 33 km C) 36 km D) 11 km
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Jeżeli 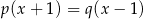 to
to
A) 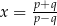 , gdy
, gdy 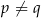 B)
B) 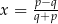 , gdy
, gdy 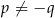
C) 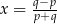 , gdy
, gdy 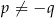 D)
D) 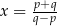 , gdy
, gdy 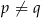
Suma liczb  i
i 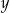 jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 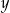 są różnych znaków. są różnych znaków. | P | F |
| Na osi liczbowej odległość każdej z tych liczb od 0 jest nie mniejsza od 1. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe. Liczba osi symetrii figury przedstawionej na rysunku jest równa

A) 4 B) 0 C) 2 D) 1
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
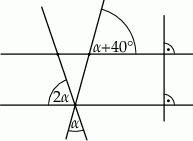
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
A) 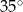 B)
B) 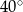 C)
C) 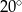 D)
D) 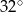
W pierwszym pudełku jest 6 kul zielonych i 9 czerwonych, a w drugim są 4 kule zielone i 6 czarnych. Losujemy po jednej kuli z każdego z pudełek. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania zielonej kuli z pierwszego pudełka jest większe, niż prawdopodobieństwo wylosowania zielonej kuli z drugiego pudełka? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w pierwszym pudełku jest więcej kul zielonych niż w drugim pudełku. |
| B) | w każdym z pudełek kule zielone stanowią taki sam procent pozostałych kul. |
| C) | w pierwszym pudełku jest tyle samo kul zielonych, ile jest kul czarnych w drugim pudełku. |
W układzie współrzędnych narysowano wykres funkcji i zaznaczono jego punkty przecięcia z osiami układu.
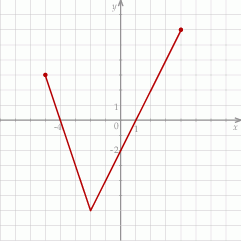
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 0 dla dwóch argumentów: 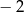 i 1. i 1. | P | F |
Dla wszystkich argumentów większych od 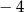 i jednocześnie mniejszych od 1 funkcja przyjmuje wartości ujemne. i jednocześnie mniejszych od 1 funkcja przyjmuje wartości ujemne. | P | F |
Jeden z kątów trójkąta prostokątnego 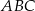 ma miarę
ma miarę 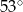 . Trójkąt
. Trójkąt 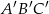 jest podobny do trójkąta
jest podobny do trójkąta 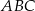 w skali 3:2.
w skali 3:2.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Miara najmniejszego kąta trójkąta 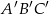 jest równa
jest równa
A) 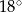 B)
B) 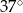 C)
C) 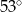 D)
D) 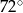
Podstawy trapezu mają długości 9 cm i 12 cm, a jedno z jego ramion ma długość 7 cm.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód tego trapezu może być równy 56 cm. | P | F |
Pole tego trapezu może być równe 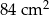 . . | P | F |
Na rysunku przedstawiono okrąg o środku 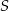 i kąt wpisany o mierze
i kąt wpisany o mierze 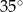 .
.
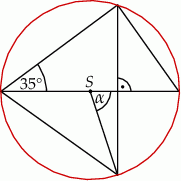
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 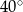 B)
B) 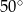 C)
C) 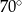 D)
D) 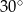
Przyprostokątne trójkąta prostokątnego mają długości 5 cm i 12 cm.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Najkrótsza wysokość tego trójkąta ma długość
A) 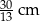 B) 5 cm C) 12 cm D)
B) 5 cm C) 12 cm D) 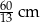
Na wysokości 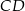 trójkąta równobocznego
trójkąta równobocznego  o boku długości 4 zbudowano kwadrat
o boku długości 4 zbudowano kwadrat  .
.
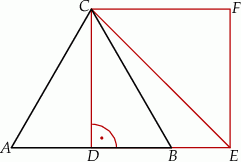
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta  jest równe
jest równe
A) 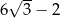 B)
B) 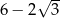 C)
C) 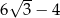 D)
D) 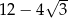
Dwie metalowe kule o promieniach po 2 cm przetopiono z kulami o promieniach 1 cm. Otrzymano jedną kulę o promieniu 3 cm. Ile łącznie kul przetopiono? Wybierz odpowiedź spośród podanych.
A) 11 B) 13 C) 1 D) 3
Z zestawu czterech liczb usunięto jedną liczbę i pozostały liczby 4, 6, 9. Mediana otrzymanego w ten sposób zestawu trzech liczb jest mniejsza od mediany początkowego zestawu czterech liczb. Uzasadnij, że usunięta liczba jest większa od 6.
W pudełku znajduje się 420 cukierków w trzech kolorach. Cukierków zielonych jest czterokrotnie więcej niż czerwonych, a cukierków żółtych jest trzy razy mniej niż zielonych i czerwonych razem. Ile cukierków czerwonych należy dołożyć do pudełka, aby stanowiły one 40% cukierków w pudełku?
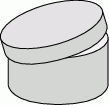
Dolna część pudełka na kapelusze ma wysokość 14 cm i średnicę podstawy równą 24 cm. Pokrywka tego pudełka ma średnicę o 8 mm większą, niż jego dolna część oraz wysokość równą 4 cm. Oblicz jakie jest pole powierzchni tektury użytej do wykonania tego pudełka.
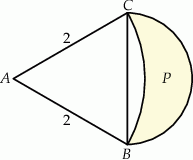
Trójkąt 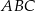 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar 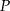 jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 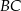 i łukiem okręgu o środku
i łukiem okręgu o środku 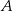 przechodzącym przez punkty
przechodzącym przez punkty 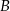 i
i 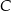 . Oblicz pole obszaru
. Oblicz pole obszaru 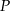 .
.