/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 25 marca 2017 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Grupa młodzieży wybrała się na spacer po lesie. W trakcie wycieczki dwukrotnie zrobiono przerwę na odpoczynek. Wykres przedstawia zależność przebytej drogi od czasu trwania spaceru.
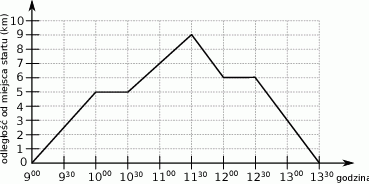
Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
A) Czas poświęcony na przerwy stanowił ponad 20% czasu całej wycieczki.
B) W trakcie wycieczki młodzież pokonała dystans 9 kilometrów.
C) W ciągu ostatniej godziny młodzież pokonała 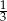 całej trasy.
całej trasy.
D) Pomiędzy przerwami młodzież pokonała dystans 7 kilometrów.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bezpośrednio przed drugą przerwą prędkość poruszania się grupy była taka sama jak tuż przed zakończeniem wycieczki. | P | F |
| W czasie pomiędzy przerwami grupa poruszała się ze stałą prędkością. | P | F |
Z cyfr 3, 4 i 5 Kasia utworzyła wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Które z poniższych zdań jest prawdziwe?
Wybierz właściwą odpowiedź spośród podanych.
A) Wszystkie liczby utworzone przez Kasię są nieparzyste.
B) Wszystkie liczby utworzone przez Kasię są podzielne przez 3.
C) Trzy liczby utworzone przez Kasię są podzielne przez 5.
D) Wśród liczb utworzonych przez Kasię są liczby podzielne przez 4.
Rozwinięcie dziesiętne ułamka jest równe 0,(285714).
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Ułamek ten jest równy
A) 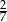 B)
B) 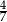 C)
C) 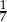 D)
D) 
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 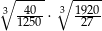 jest równa
jest równa
A) 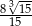 B)
B) 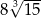 C) 8 D)
C) 8 D) 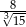
Dane są liczby  i
i 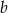 takie, że
takie, że 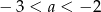 oraz
oraz 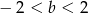 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 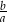 jest zawsze ujemny. jest zawsze ujemny. | P | F |
Różnica 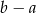 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
W układzie współrzędnych zaznaczono punkt 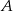 .
.
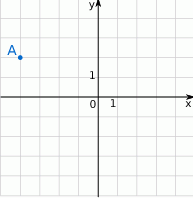
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Punkt symetryczny do punktu 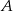 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 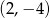 B)
B) 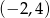 C)
C) 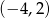 D)
D) 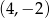
Na rysunku przedstawiono wykres pewnej funkcji.
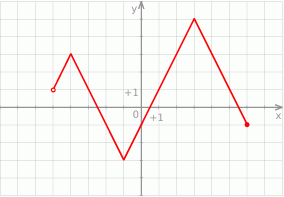
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość największą dla argumentu 4. | P | F |
| Funkcja przyjmuje wartość 0 dla czterech argumentów. | P | F |
Właściciel sklepu zyskuje 12% z wartości każdej sprzedanej pary obuwia. Ile par tenisówek, których cena wynosi 80 zł, musi sprzedać, aby zyskać 2400 zł?
Wybierz odpowiedź spośród podanych.
A) 250 B) 200 C) 240 D) 300
Cenę telewizora obniżono o 15%, a następnie o 2%. Klient kupił telewizor po obniżonej cenie i dzięki temu zapłacił o 501 zł mniej, niż zapłaciłby przed obniżkami.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Przed obniżkami ten telewizor kosztował
A) 2947 zł B) 4000 zł C) 3000 zł D) 2840 zł
Liczby  i
i 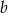 są dwucyfrowe oraz liczba
są dwucyfrowe oraz liczba 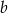 powstaje z
powstaje z  w wyniku zapisania cyfr liczby
w wyniku zapisania cyfr liczby  w odwrotnej kolejności.
w odwrotnej kolejności.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 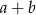 jest zawsze podzielna przez 11. jest zawsze podzielna przez 11. | P | F |
Liczba 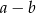 jest zawsze podzielna przez 9. jest zawsze podzielna przez 9. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 9 razy mniejsza od 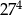 jest równa
jest równa
A) 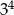 B)
B) 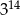 C)
C) 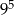 D)
D) 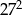
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Pole wielokąta przedstawionego na rysunku opisuje wyrażenie algebraiczne
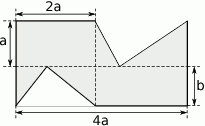
A) 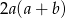 B)
B) 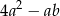 C)
C) 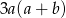 D)
D) 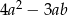
Tomek otrzymał z sześciu sprawdzianów z matematyki następujące oceny: 5, 4, 2, 3, 2, 3. Po kolejnych dwóch sprawdzianach średnia ocen Tomka ze wszystkich sprawdzianów wyniosła 3,5. Jakie oceny mógł otrzymać Tomek z ostatnich dwóch sprawdzianów?
Wybierz odpowiedź spośród podanych.
A) 4 i 4 B) 4 i 5 C) 3 i 4 D) 5 i 3
Informacja do zadań 15 i 16
W tabeli przedstawiono informacje dotyczące cen akcji trzech firm w dwóch różnych wybranych dniach tego samego roku.
| Firma | Cena 1 akcji w dniu 1 lutego | Cena 1 akcji w dniu 31 sierpnia |
| Salceson S.A. | 15 zł | 18 zł |
| Kabanos S.A. | 24 zł | 36 zł |
| Salami S.A. | 96 zł | 64 zł |
Pan Tomasz 1 lutego za 1410 zł kupił pewną liczbę akcji firm Salceson S.A. i Kabanos S.A. Wszystkie kupione akcje sprzedał 31 sierpnia za kwotę 1980 zł.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba akcji firmy Kabanos S.A, które Pan Tomasz kupił 1 lutego jest równa
A) 36 B) 18 C) 58 D) 40
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W okresie między 1 lutego a 31 sierpnia procentowy wzrost ceny akcji firmy Salceson S.A. by wyższy niż procentowy wzrost ceny akcji firmy Kabanos S.A. | P | F |
| Łączna wartość 40 akcji firmy Kabanos S.A. i 10 akcji firmy Salami S.A. była wyższa w dniu 31 sierpnia niż 1 lutego. | P | F |
Proste 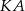 i
i 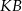 są styczne do okręgu o środku
są styczne do okręgu o środku 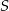 w punktach
w punktach 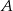 i
i 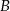 , a kąt
, a kąt 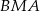 ma miarę
ma miarę 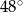 (rysunek).
(rysunek).
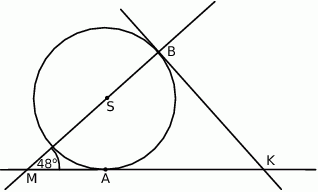
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Kąt 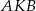 jest równy
jest równy
A) 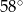 B)
B) 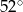 C)
C) 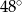 D)
D) 
Na przeciwprostokątnej trójkąta prostokątnego o przyprostokątnych długości 1 i 3 zbudowano prostokąt o jednym boku długości 1.
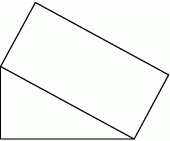
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość przekątnej tego prostokąta jest równa
A) 3 B) 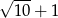 C)
C) 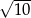 D)
D) 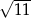
Ściany sześciennej kostki ponumerowano liczbami od 1 do 6. Następnie w sposób losowy wybrano jedną z krawędzi tego sześcianu.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Prawdopodobieństwo zdarzenia polegające na tym, że wylosowana krawędź jest krawędzią ściany z numerem 6 jest równe
A) 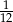 B)
B) 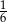 C)
C) 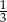 D)
D) 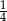
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 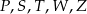 są środkami jego krawędzi.
są środkami jego krawędzi.
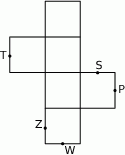
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Po złożeniu sześcianu z tej siatki punkt 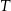 pokryje się z punktem
pokryje się z punktem
A) 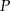 B)
B) 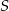 C)
C) 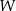 D)
D) 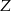
W wycinek koła o kącie 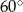 wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
wpisano okrąg o promieniu 2 cm. Oblicz pole tego wycinka.
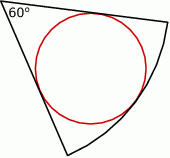
Z sześcianu zbudowanego z 125 małych sześcianów o krawędzi 1 cm usunięto z każdego narożnika po jednym małym sześcianie (patrz rysunek). Oblicz pole powierzchni powstałej bryły.
Dwie maszyny produkcyjne miały wyprodukować łącznie 10240 plastikowych pojemników. Po zakończeniu produkcji okazało się, że jedna z maszyn przekroczyła plan o 15%, a druga o 20% i w sumie maszyny wyprodukowały 12096 pojemników. Ile pojemników wyprodukowała każda z maszyn?

