/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 21 marca 2015 Czas pracy: 90 minut
Informacja do zadań 1 – 3
Pracownik salonu samochodowego otrzymuje premię za każdy sprzedany samochód w wysokości 300 zł oraz dodatkowo 0,5% kwoty za jaką sprzedano samochód.
Pracownik salonu sprzedał trzy samochody za łączną kwotę 84 000 zł. Ile premii otrzyma za sprzedaż tych samochodów? Wybierz odpowiedź spośród podanych.
A) 1320 zł B) 720 zł C) 1020 zł D) 942 zł
Pracownik salonu sprzedał 5 samochodów i otrzymał za to 2335 zł premii. Jaka była łączna kwota, za którą sprzedano te samochody? Wybierz odpowiedź spośród podanych.
A) 467 000 zł B) 407 000 zł C) 417 500 zł D) 167 000 zł
Pracownik salonu sprzedał pewną liczbę samochodów, przy czym żaden z nich nie kosztował więcej niż 40 000 i otrzymał za to 3848 zł premii.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pracownik mógł sprzedać 7 samochodów. | P | F |
| Pracownik mógł sprzedać 13 samochodów. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczbą mniejszą od 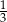 jest
jest
A) 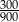 B)
B) 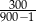 C)
C) 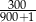 D)
D) 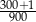
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
W torbie z cukierkami co trzeci cukierek jest czerwony, co piąty jest zielony, dwanaście cukierków jest żółtych, a wszystkich pozostałych cukierków jest dwa razy więcej niż zielonych. W torbie jest
A) 120 cukierków. B) 150 cukierków. C) 180 cukierków. D) 240 cukierków.
Dane są liczby 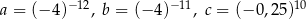 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczby te uporządkowane od najmniejszej do największej to:
A) 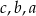 B)
B) 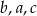 C)
C) 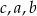 D)
D) 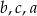
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 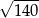 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 11 i 12 C) 12 i 20 D) 30 i 40
Dane są liczby  i
i 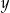 spełniające warunek:
spełniające warunek: 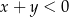 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 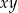 nie może być dodatnia. nie może być dodatnia. | P | F |
Liczba 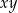 może być równa 0. może być równa 0. | P | F |
Brukarz układał kostkę brukową. Wykres przedstawia liczbę ułożonych kostek w zależności od czasu w trakcie ośmiogodzinnego dnia pracy.
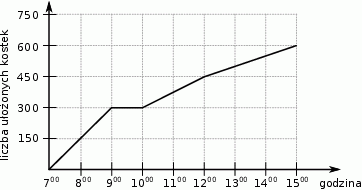
Na podstawie wykresu wybierz zdanie fałszywe.
A) O godzinie 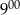 brukarz rozpoczął godzinną przerwę.
brukarz rozpoczął godzinną przerwę.
B) Od 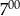 do
do 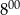 brukarz ułożył więcej kostek niż od
brukarz ułożył więcej kostek niż od 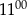 do
do 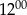 .
.
C) W czwartej i w piątej godzinie brukarz ułożył taką samą liczbę kostek.
D) Przez ostatnie trzy godziny pracy brukarz ułożył 100 kostek.
W pudełku są tylko kule białe i czarne, przy czym kul czarnych jest o 5 więcej niż kul białych, a prawdopodobieństwo wylosowania kuli białej jest dwa razy mniejsze, niż prawdopodobieństwo wylosowania kuli czarnej. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest więcej niż 12 kul. | P | F |
| Po dołożeniu do pudełka 3 kul czarnych, prawdopodobieństwo wylosowania kuli białej będzie 3 razy mniejsze niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
Rowerzysta pokonuje trasę między miejscowościami 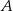 i
i 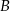 w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta
w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta 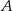 tak, aby obaj dotarli do miasta
tak, aby obaj dotarli do miasta 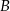 w tym samym momencie? Wybierz odpowiedź spośród podanych.
w tym samym momencie? Wybierz odpowiedź spośród podanych.
A) O 64 minuty. B) O 84 minut. C) O 96 minut. D) O 144 minuty.
Wojtek ma w skarbonce  monet pięciozłotowych i
monet pięciozłotowych i 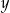 monet dwuzłotowych. Liczby
monet dwuzłotowych. Liczby  i
i 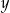 spełniają równanie
spełniają równanie 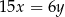 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 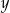 może być równa 17. może być równa 17. | P | F |
| Kwota oszczędności zgromadzonych w dwuzłotówkach jest równa kwocie oszczędności zgromadzonych w pięciozłotówkach. | P | F |
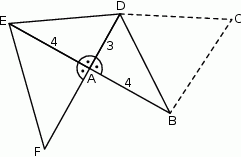
W trapezie 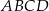 punkt
punkt 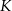 jest środkiem ramienia
jest środkiem ramienia 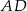 , a punkt
, a punkt 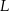 jest środkiem podstawy
jest środkiem podstawy 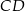 .
.
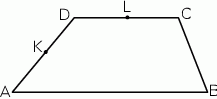
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 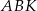 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 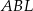 . . | P | F |
Pole trójkąta 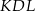 jest dwa razy mniejsze od pola trójkąta jest dwa razy mniejsze od pola trójkąta 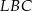 . . | P | F |
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji.
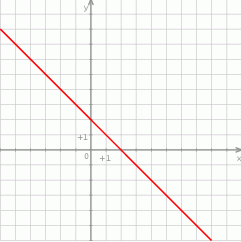
Które z poniższych zdań jest fałszywe? Wybierz odpowiedź spośród podanych.
A) Dla argumentu 3 wartość funkcji jest równa 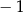 .
.
B) Funkcja przyjmuje wartość 3 dla argumentu 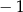 .
.
C) Dla argumentów większych od 2 wartości funkcji są dodatnie.
D) Wartość funkcji jest równa 4 dla argumentu 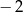 .
.
W tabeli podano oceny czterech uczniów, oraz obliczone na podstawie tych danych: średnią i medianę.
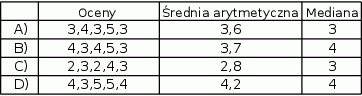
Wskaż, w którym wierszu tabeli popełniono błąd w obliczeniach.
Informacja do zadań 16 i 17
Antek narysował kwadrat położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego kwadraty rysował w taki sposób, że kolejny kwadrat powstaje z poprzedniego poprzez wykonanie trzech czynności: odbicia symetrycznego względem osi 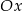 , przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi
, przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi 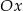 (rysunek 2.).
(rysunek 2.).
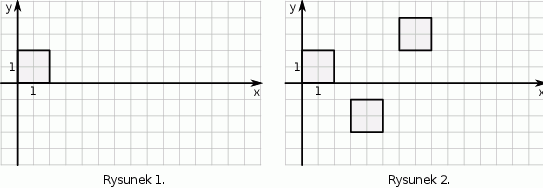
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Antek narysował w opisany sposób czwarty kwadrat. Współrzędna  środka tego kwadratu jest równa
środka tego kwadratu jest równa
A) 8 B) 9 C) 10 D) 11
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli współrzędne środka ostatniego narysowanego kwadratu są równe 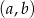 i
i 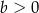 , to współrzędne środka kolejnego kwadratu będą równe
, to współrzędne środka kolejnego kwadratu będą równe
A) 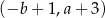 B)
B) 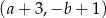 C)
C) 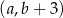 D)
D) 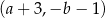
Tosia wykonała szkielet prostopadłościanu. Układała i sklejała ze sobą kolejno drewniane klocki sześcienne o krawędzi 3 cm wzdłuż każdej krawędzi prostopadłościennego pudełka o wymiarach: 18 cm, 24 cm, 18 cm. Na rysunku przedstawiono część wykonanego szkieletu.
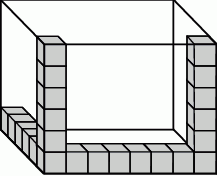
Ile klocków łącznie zużyła Tosia na wykonanie całego szkieletu? Wybierz odpowiedź spośród podanych.
A) 72 B) 64 C) 68 D) 60
Hela rysuje siatkę ostrosłupa, którego podstawą jest prostokątny trójkąt równoramienny 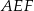 .
.
Czy trójkąt równoboczny 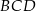 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | odcinki 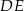 i i 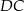 mają różne długości. mają różne długości. |
| B) | odcinki 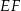 i i 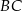 mają różne długości. mają różne długości. |
| C) | odcinki 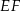 i i 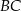 mają równe długości. mają równe długości. |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Suma pól powierzchni 27 sześcianów, z których każdy ma krawędź długości 1, jest taka sama jak pole powierzchni jednego sześcianu o krawędzi długości
A) 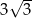 B) 3 C)
B) 3 C) 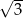 D) 9
D) 9
Cena godziny korzystania z kręgielni wynosi 42 zł. Można jednak kupić miesięczną kartę rabatową za 50 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 4 godziny gry płaci się 35 złotych za godzinę, a za każdą następną godzinę – 40 złotych. Ela kupiła kartę rabatową i korzystała z kręgielni przez 12 godzin. Czy zakup karty był dla Eli opłacalny? Zapisz obliczenia.
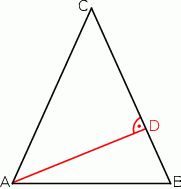
Odcinek 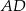 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 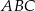 , w którym
, w którym 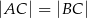 . Udowodnij, że
. Udowodnij, że 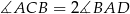 .
.
W kostce mającej kształt sześcianu ścięto wszystkie naroża, w ten sposób że otrzymane w narożach trójkąty są trójkątami równobocznymi o boku długości 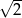 , a wszystkie pozostałe krawędzie bryły mają długość 1. Oblicz objętość otrzymanej bryły.
, a wszystkie pozostałe krawędzie bryły mają długość 1. Oblicz objętość otrzymanej bryły.