/Gimnazjum/Egzamin gimnazjalny
Egzamin Gimnazjalny
z Matematyki 11 kwietnia 2019 Czas pracy: 90 minut
W dwóch litrowych butelkach była woda. Na wykresie przedstawiono, jak zmieniała się objętość wody w pierwszej butelce w trakcie przelewania do niej całej zawartości drugiej butelki.
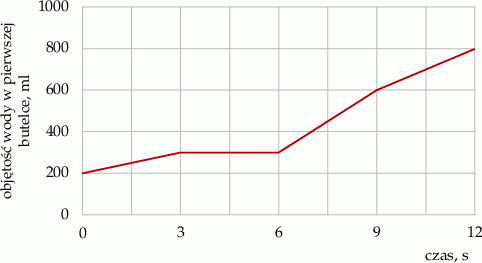
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na początku w pierwszej butelce było 200 ml wody, a w drugiej butelce było 800 ml wody. | P | F |
| W czasie ostatnich trzech sekund przelano 200 ml wody. | P | F |
Zosia zebrała 2 kg malin i wsypała je do trzech takich samych pojemników. Masa pustego pojemnika była równa 0,05 kg. Pierwszy pojemnik z malinami miał masę 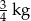 , a masa drugiego pojemnika z malinami była równa 0,70 kg.
, a masa drugiego pojemnika z malinami była równa 0,70 kg.
Ile malin wsypała Zosia do trzeciego pojemnika?
Wybierz właściwą odpowiedź spośród podanych.
A) 0,45 kg B) 0,55 kg C) 0,60 kg D) 0,65 kg
Na osi liczbowej zaznaczono dwa punkty 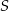 i
i 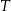 . Odcinek
. Odcinek 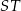 podzielono na 12 równych części.
podzielono na 12 równych części.
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość odcinka 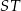 jest równa
jest równa
A) 1750 B) 1500 C) 1250 D) 1000
Dane są liczby:
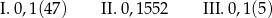
Dla których liczb zaokrąglenie do części setnych jest równe 0,15? Wybierz właściwą odpowiedź spośród podanych.
A) I, II i III B) Tylko I i II C) Tylko I i III D) Tylko I E) Tylko III
Kacper zabrał na wycieczkę dwa razy mniej pieniędzy niż Wojtek. Kacper wydał połowę swoich pieniędzy, a Wojtek wydał 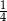 swoich.
swoich.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kacper wydał tyle samo pieniędzy, ile wydał Wojtek. | P | F |
| Po wycieczce Kacprowi zostało trzy razy mniej pieniędzy niż Wojtkowi. | P | F |
Para liczb 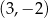 spełnia układ równań
spełnia układ równań
A) 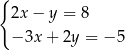 B)
B) 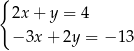
C) 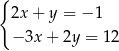 D)
D) 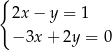
Dane są liczby 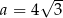 ,
, 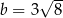 ,
, 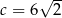 ,
, 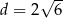 .
.
Która zależność jest prawdziwa? ? Wybierz właściwą odpowiedź spośród podanych.
A) 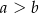 B)
B) 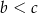 C)
C) 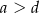 D)
D) 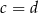
Do zbiornika wypełnionego w 65% wodą dolano 12 litrów wody. Teraz woda wypełnia 80% pojemności zbiornika.
Ile litrów wody jest teraz w zbiorniku? Wybierz właściwą odpowiedź spośród podanych.
A) 52 litry B) 64 litry C) 77 litrów D) 80 litrów
Dane są trzy liczby:
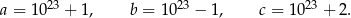
Które z tych liczb są podzielne przez 3? Wybierz właściwą odpowiedź spośród podanych.
A) Tylko liczby  i
i 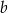 . B) Tylko liczba
. B) Tylko liczba 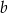 . C) Tylko liczby
. C) Tylko liczby 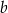 i
i  . D) Tylko liczba
. D) Tylko liczba  .
.
Dany jest zestaw liczb: 4, 9, 11, 15, 21. Do podanych liczb dopisano jeszcze jedną liczbę i wtedy średnia arytmetyczna nowego zestawu liczb zwiększyła się o 1.
Która liczba została dopisana? Wybierz właściwą odpowiedź spośród podanych.
A) 10 B) 12 C) 13 D) 18
Informacja do zadań 11 i 12
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.

Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.
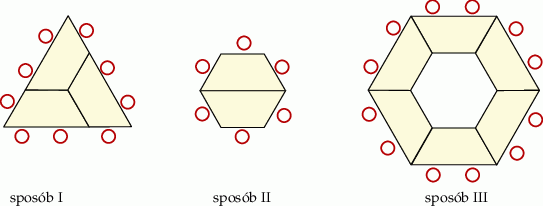
W ośrodku jest 36 stolików. Postanowiono je ustawić w jeden z trzech sposobów pokazanych na powyższych rysunkach.
Które z poniższych zdań jest fałszywe? Wybierz właściwą odpowiedź spośród podanych.
A) Po ustawieniu wszystkich stolików w sposób I uzyska się tyle samo miejsc siedzących, ile powstaje po ustawieniu wszystkich stolików w sposób II.
B) Najmniejszą liczbę miejsc siedzących uzyska się po ustawieniu wszystkich stolików w sposób III.
C) Po ustawieniu wszystkich stolików w sposób I uzyska się 108 miejsc siedzących.
D) Po ustawieniu wszystkich stolików w sposób II uzyska się 96 miejsc siedzących.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąty trapezu przedstawionego na rysunku 1 mają miary: 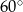 , , 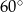 , , 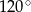 , , 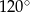 . . | P | F |
| Krótsza podstawa tego trapezu jest 2 razy krótsza od jego dłuższej podstawy. | P | F |
W układzie współrzędnych zaznaczono trzy punkty 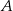 ,
, 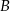 ,
,  o współrzędnych całkowitych, jak na rysunku.
o współrzędnych całkowitych, jak na rysunku.
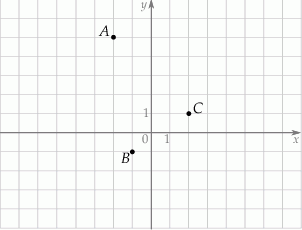
Które z tych punktów należą do wykresu funkcji określonej wzorem 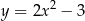 ?
?
Wybierz właściwą odpowiedź spośród podanych.
A) 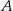 ,
, 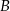 i
i 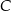 . B) Tylko
. B) Tylko 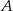 i
i 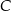 . C) Tylko
. C) Tylko 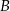 i
i 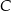 . D) Tylko
. D) Tylko 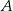 i
i 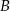 .
.
Czy 18% liczby 15 jest większe niż 15% liczby 18? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | 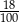 to więcej niż to więcej niż 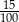 . . |
| B) | 1% liczby 15 to mniej niż 1% liczby 18. |
| C) | 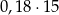 to tyle samo, ile to tyle samo, ile 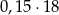 . . |
Punkty 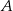 i
i 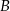 są środkami boków kwadratu o polu
są środkami boków kwadratu o polu 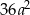 .
.
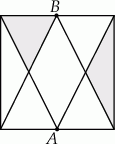
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Suma pól zacieniowanych części kwadratu jest równa
A) 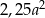 B)
B) 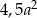 C)
C) 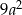 D)
D) 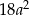
Na dwóch bokach trójkąta prostokątnego 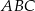 zbudowano kwadraty. Pole kwadratu zbudowanego na boku
zbudowano kwadraty. Pole kwadratu zbudowanego na boku 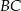 jest równe 169, a pole kwadratu zbudowanego na boku
jest równe 169, a pole kwadratu zbudowanego na boku 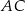 jest równe 25.
jest równe 25.
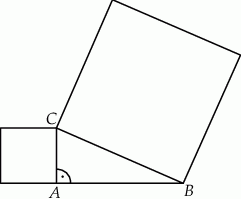
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Bok 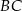 ma długość 13. ma długość 13. | P | F |
Jeżeli zbudujemy kwadrat na boku 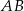 , to jego pole będzie równe 144. , to jego pole będzie równe 144. | P | F |
Pole ćwiartki koła przedstawionej na rysunku jest równe 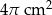 .
.
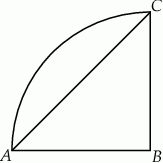
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta 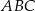 jest równe
jest równe
A) 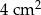 B)
B) 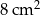 C)
C) 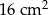 D)
D) 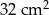
Prostokątna ramka ma szerokość 2 cm oraz 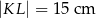 ,
, 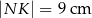 (patrz rysunek).
(patrz rysunek).
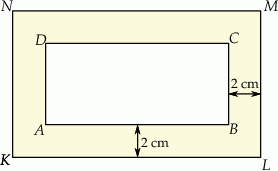
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prostokąty 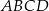 i i 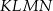 są podobne. są podobne. | P | F |
Obwód prostokąta 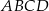 jest o 8 cm mniejszy od obwodu prostokąta jest o 8 cm mniejszy od obwodu prostokąta 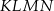 . . | P | F |
Ostrosłup i graniastosłup mają takie same podstawy. Obie bryły mają łącznie 25 wierzchołków.
Ile wierzchołków ma ostrosłup? Wybierz właściwą odpowiedź spośród podanych.
A) 6 B) 8 C) 9 D) 10
Z sześcianu o objętości 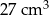 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu.
usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni powstałej bryły jest równe
A) 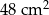 B)
B) 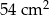 C)
C) 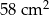 D)
D) 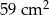
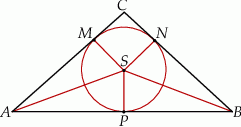
W trójkąt równoramienny 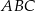 (
(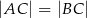 ) wpisano okrąg o środku
) wpisano okrąg o środku 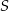 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 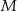 ,
, 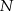 i
i 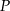 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 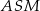 i
i  są przystające.
są przystające.
Na statku wycieczkowym są 33 miejsca dla pasażerów. Uczniowie klas IIIa i IIIb planują wycieczkę tym statkiem. W każdej z tych klas jest mniej niż 33 uczniów. Aby wszystkie miejsca dla pasażerów były na statku zajęte, należy do wszystkich uczniów klasy IIIa dołączyć 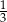 uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć
uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć 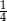 uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas?
uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas?
Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.
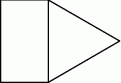
Pole narysowanego trójkąta jest równe 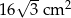 , a pole prostokąta jest równe
, a pole prostokąta jest równe 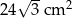 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.

