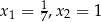/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 1526830

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie: 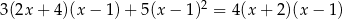2 3(2x + 4)(x− 1)+ 5(x − 1) = 4(x + 2)(x − 1) .

Rozwiązanie

Sposób I

Zauważmy, że każdy składnik w danym równaniu zeruje się dla 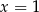x = 1 , więc jest to jedno z rozwiązań tego równania. Jeżeli natomiast 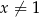x ⁄= 1 , to możemy równanie podzielić stronami przez (x − 1) .

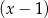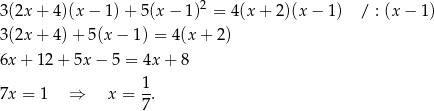
2 3(2x + 4)(x − 1 )+ 5(x − 1) = 4(x + 2)(x − 1) / : (x − 1) 3(2x + 4) + 5(x − 1) = 4(x+ 2) 6x + 12 + 5x − 5 = 4x + 8 1 7x = 1 ⇒ x = --. 7

Sposób II

Przekształcamy podane równanie:

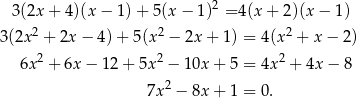
3(2x + 4)(x − 1 )+ 5(x − 1)2 = 4(x + 2)(x − 1 ) 3(2x 2 + 2x− 4)+ 5(x2 − 2x + 1) = 4(x 2 + x − 2) 2 2 2 6x + 6x − 1 2+ 5x − 10x + 5 = 4x + 4x − 8 7x2 − 8x + 1 = 0.

Pierwiastki obliczamy ze wzoru z Δ –tą:

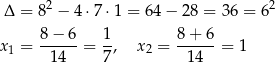
Δ = 82 − 4 ⋅7⋅ 1 = 64 − 28 = 3 6 = 62 x = 8-−-6-= 1-, x = 8-+-6-= 1 1 14 7 2 14

 
Odpowiedź: x1 = 17,x2 = 1

Wersja PDF