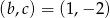Zadanie nr 1618068
Dane jest równanie 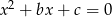 z niewiadomą
z niewiadomą  . Wyznacz wartości
. Wyznacz wartości 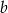 i
i  tak, by były one rozwiązaniami danego równania.
tak, by były one rozwiązaniami danego równania.
Rozwiązanie
Po pierwsze sprawdzamy, kiedy dane równanie ma rozwiązania
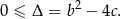
Teraz rozpatrzmy osobno przypadek 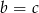 . Mamy wtedy równanie
. Mamy wtedy równanie
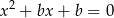
i liczba 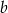 ma być jego pierwiastkiem. Mamy stąd
ma być jego pierwiastkiem. Mamy stąd
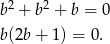
Zatem 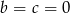 lub
lub 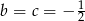 . Łatwo sprawdzić, że w obu przypadkach mamy
. Łatwo sprawdzić, że w obu przypadkach mamy 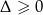 .
.
Załóżmy teraz, że 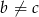 .
.
Sposób I
Na mocy wzorów Viéte’a mamy
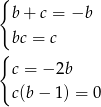
Jeżeli 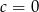 to otrzymujemy
to otrzymujemy 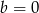 , co jest sprzeczne z założeniem
, co jest sprzeczne z założeniem 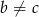 . Zatem
. Zatem 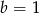 i wtedy
i wtedy 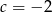 . Łatwo sprawdzić, że para ta spełnia warunek
. Łatwo sprawdzić, że para ta spełnia warunek 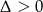 .
.
Sposób II
Jeżeli liczby 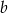 i
i  są dwoma różnymi pierwiastkami danego trójmianu
są dwoma różnymi pierwiastkami danego trójmianu 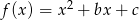 to musi on mieć postać
to musi on mieć postać
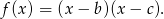
Mamy stąd równanie
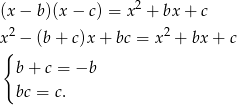
Otrzymany układ równań rozwiązujemy tak samo jak w pierwszym sposobie.
Sposób III
Z informacji o tym, że liczby 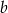 i
i  są rozwiązaniami danego równania otrzymujemy układ równań
są rozwiązaniami danego równania otrzymujemy układ równań
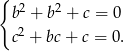
Odejmujemy teraz od pierwszego równania drugie i mamy
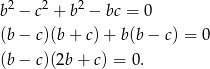
Założyliśmy, że 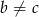 , więc mamy stąd
, więc mamy stąd 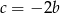 . Wtedy z pierwszego równania układu mamy
. Wtedy z pierwszego równania układu mamy
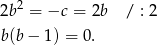
Jeżeli 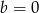 to
to 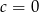 i mamy sprzeczność z założeniem
i mamy sprzeczność z założeniem 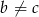 . Zatem
. Zatem 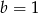 i
i 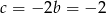 . Łatwo sprawdzić, że para ta spełnia warunek
. Łatwo sprawdzić, że para ta spełnia warunek 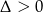 .
.
Odpowiedź: 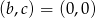 lub
lub 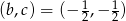 lub
lub