/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 1767312

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie liczby całkowite 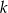k , dla których iloczyn dwóch różnych miejsc zerowych funkcji 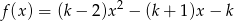f (x) = (k− 2)x2 − (k+ 1)x − k jest liczbą całkowitą.

Rozwiązanie

Jeżeli mają być dwa miejsca zerowe, to funkcja musi być kwadratowa, czyli 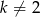k ⁄= 2 . Sprawdźmy kiedy funkcja ma dwa pierwiastki.

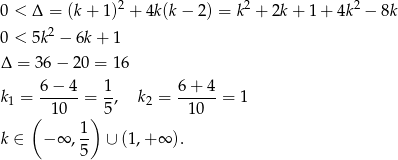
2 2 2 0 < Δ = (k+ 1) + 4k(k− 2) = k + 2k + 1 + 4k − 8k 0 < 5k2 − 6k + 1 Δ = 36− 20 = 16 6 − 4 1 6 + 4 k1 = ------= -, k2 = ------= 1 ( 10 ) 5 10 k ∈ −∞ , 1 ∪ (1,+ ∞ ). 5

Na mocy wzorów Viète’a wiemy, że iloczyn pierwiastków jest równy

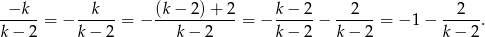
-−k--- --k--- (k-−-2)-+-2 k−-2-- --2--- --2--- k− 2 = − k− 2 = − k − 2 = − k− 2 − k− 2 = − 1 − k − 2 .

Przekształcenie było trochę trickowe, ale chyba jest jasne po co je zrobiliśmy – teraz w liczniku ułamka jest 2, więc ułamek będzie liczbą całkowitą tylko wtedy, gdy w mianowniku jest jedna z liczb -2,2,-1,1. Daje to nam odpowiednio 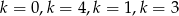k = 0,k = 4,k = 1,k = 3 . Tylko 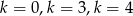k = 0 ,k = 3,k = 4 spełniają warunek z Δ -ą.  
Odpowiedź: k = 0∨ k = 3 ∨ k = 4

Wersja PDF