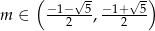/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 1812630

Dodaj do ulubionych
Dodaj do rozwiązanych

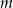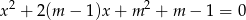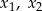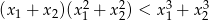Wyznacz wszystkie wartości parametru m , dla których równanie x 2 + 2(m − 1)x + m 2 + m − 1 = 0 ma dwa różne pierwiastki rzeczywiste x1, x2 takie, że (x1 + x2)(x21 + x22) < x 31 + x 32 .

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki.

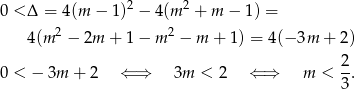
2 2 0 < Δ = 4(m − 1) − 4(m + m − 1) = 4 (m 2 − 2m + 1− m 2 − m + 1) = 4(− 3m + 2) 0 < − 3m + 2 ⇐ ⇒ 3m < 2 ⇐ ⇒ m < 2-. 3

Przy tym założeniu możemy skorzystać ze wzorów Viète’a.

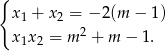
{ x 1 + x 2 = − 2(m − 1) x 1x 2 = m 2 + m − 1.

Dana nierówność przyjmuje więc postać.

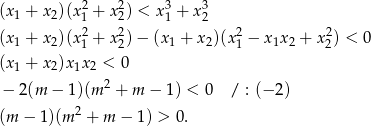
(x + x )(x2+ x2) < x3 + x3 1 2 1 2 1 2 (x 1 + x 2)(x21 + x22)− (x1 + x2)(x21 − x1x2 + x22) < 0 (x + x )x x < 0 1 2 1 2 − 2(m − 1)(m 2 + m − 1 ) < 0 / : (− 2) 2 (m − 1)(m + m − 1 ) > 0.

Rozkładamy trójmian w drugim nawiasie.

Δ = 1 + 4 = 5 √ -- √ -- −-1-−---5- −-1-+---5- m = 2 ≈ − 1,6 ∨ m = 2 ≈ 0,6.

Interesująca nas nierówność ma więc postać

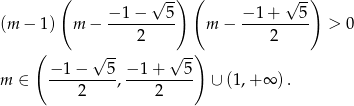
( √ --) ( √ -) −1 − 5 − 1+ 5 (m − 1) m − ---------- m − ---------- > 0 2 2 ( √ -- √ -) m ∈ −1-−---5-, −-1+---5- ∪ (1,+ ∞ ). 2 2

Uwzględniając warunek z 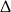Δ -ą mamy

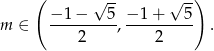
( √ -- √ --) − 1 − 5 −1 + 5 m ∈ ---------, ---------- . 2 2

 
Odpowiedź: ( √ - √-) m ∈ −1−--5, −-1+-5- 2 2

Wersja PDF