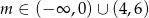/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 1946241

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 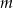m , dla których równanie 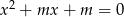2 x + mx + m = 0 ma dwa różne pierwiastki takie, że ich iloczyn jest mniejszy od 6.

Rozwiązanie

Najpierw sprawdźmy, kiedy równanie ma dwa różne pierwiastki. Liczymy

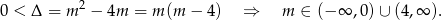
2 0 < Δ = m − 4m = m(m − 4) ⇒ m ∈ (− ∞ ,0)∪ (4,∞ ).

Iloczyn pierwiastków obliczamy ze wzorów Viète’a.

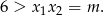
6 > x x = m . 1 2

Z obu otrzymanych nierówności mamy

m ∈ (− ∞ ,0) ∪ (4,6).

 
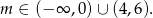
Odpowiedź: m ∈ (− ∞ ,0)∪ (4 ,6)

Wersja PDF