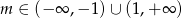Zadanie nr 2128188
Wyznacz wszystkie wartości parametru 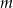 , dla których równanie
, dla których równanie
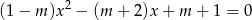
ma przynajmniej jedno rozwiązanie ujemne.
Rozwiązanie
Jeżeli 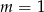 to mamy równanie
to mamy równanie
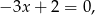
które ma tylko rozwiązanie dodatnie.
Jeżeli 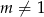 to mamy równanie kwadratowe i liczymy
to mamy równanie kwadratowe i liczymy 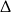 -ę, żeby ustalić kiedy ma ono pierwiastki.
-ę, żeby ustalić kiedy ma ono pierwiastki.
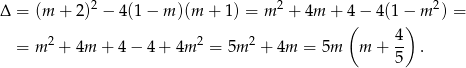
Widać zatem, że 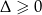 dla
dla 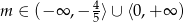 .
.
Pozostało ustalić, kiedy przynajmniej jeden z pierwiastków jest ujemny.
Sposób I
Zamiast sprawdzać, kiedy jeden z pierwiastków jest ujemny sprawdźmy warunek przeciwny, czyli warunek, że oba pierwiastki 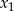 i
i 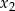 są nieujemne. Tak będzie jeżeli
są nieujemne. Tak będzie jeżeli 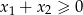 i
i 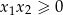 . Na mocy wzorów Viète’a możemy te nierówności zapisać w postaci:
. Na mocy wzorów Viète’a możemy te nierówności zapisać w postaci:
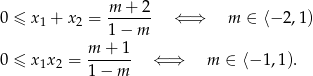
Zatem oba pierwiastki są nieujemne dla 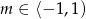 . To oznacza, że przynajmniej jeden z nich jest ujemny dla
. To oznacza, że przynajmniej jeden z nich jest ujemny dla 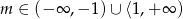 . Uwzględniając przypadek
. Uwzględniając przypadek 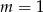 i warunek z
i warunek z  -ą otrzymujemy
-ą otrzymujemy
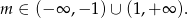
Sposób II
Zastanówmy się jaki może być znak 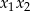 . Jeżeli
. Jeżeli 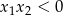 to na pewno jeden z pierwiastków będzie ujemny. Tak będzie, gdy
to na pewno jeden z pierwiastków będzie ujemny. Tak będzie, gdy
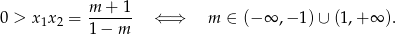
Jeżeli natomiast 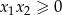 , czyli
, czyli 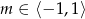 , to liczby
, to liczby 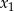 i
i 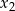 mają ten sam znak (lub są równe zero). Zatem jedna z nich będzie ujemna dokładnie wtedy, gdy
mają ten sam znak (lub są równe zero). Zatem jedna z nich będzie ujemna dokładnie wtedy, gdy 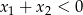 . Tak będzie, gdy
. Tak będzie, gdy
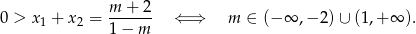
Podsumowując (i zaglądając do wcześniej uzyskanych warunków z 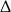 -ą i
-ą i 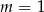 ), jeden pierwiastek jest ujemny dla
), jeden pierwiastek jest ujemny dla
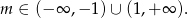
Odpowiedź: