/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 2188541

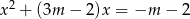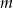Dane jest równanie 2 x + (3m − 2)x = −m − 2 z niewiadomą x . Sformułuj warunki, jakie powinien spełniać parametr m , by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.

Wersja PDF

Rozwiązanie

Zapiszmy równanie w postaci

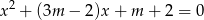
2 x + (3m − 2)x + m + 2 = 0

i rozpocznijmy od sprawdzenia, kiedy ma ono dwa pierwiastki.

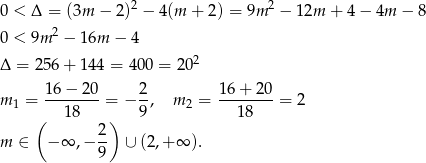
2 2 0 < Δ = (3m − 2) − 4(m + 2) = 9m − 12m + 4 − 4m − 8 0 < 9m 2 − 16m − 4 Δ = 256+ 144 = 4 00 = 202 16 − 20 2 16+ 20 m 1 = --------= − -, m2 = --------= 2 ( 18 ) 9 18 m ∈ − ∞ ,− 2- ∪ (2,+ ∞ ). 9

Pozostało sprawdzić, kiedy suma odwrotności pierwiastków jest dodatnia. Będziemy przy tym korzystać ze wzorów Viète’a:

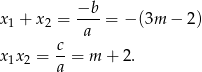
−b x1 + x2 = -a--= − (3m − 2) c x1x2 = --= m + 2. a

Liczymy teraz sumę odwrotności pierwiastków

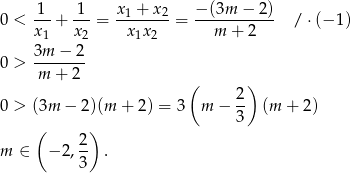
1 1 x + x − (3m − 2) 0 < --+ ---= -1----2-= ----------- / ⋅(− 1) x1 x2 x1x 2 m + 2 3m-−-2- 0 > m + 2 ( 2 ) 0 > (3m − 2)(m + 2) = 3 m − -- (m + 2) ( ) 3 2 m ∈ − 2 ,-- . 3

W połączeniu z warunkiem z 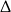Δ -ą daje to

( 2 ) m ∈ − 2,− -- . 9

 
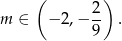
Odpowiedź: ( ) m ∈ − 2,− 29

Wersja PDF