Zadanie nr 2203831
Dane jest równanie 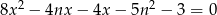 z niewiadomą
z niewiadomą  i parametrem
i parametrem  .
.
- Wyznacz wszystkie wartości
 , dla których suma odwrotności pierwiastków tego równania jest równa
, dla których suma odwrotności pierwiastków tego równania jest równa 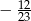 .
. - Wykaż, że jeżeli
 jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
Rozwiązanie
Zapiszmy równanie w postaci
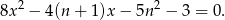
Na początku sprawdźmy kiedy równanie ma pierwiastki
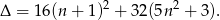
Widać, że wyrażenie to jest dodatnie, więc równanie ma zawsze dwa pierwiastki 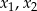 . Ponadto, na mocy wzorów Viète’a mamy
. Ponadto, na mocy wzorów Viète’a mamy
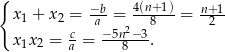
- Musimy rozwiązać równanie
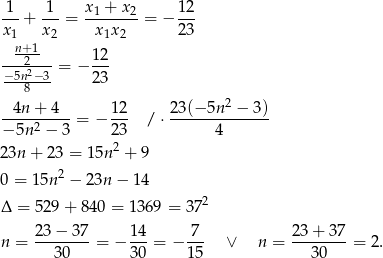
Odpowiedź: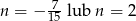
- Liczymy sumę kwadratów pierwiastków
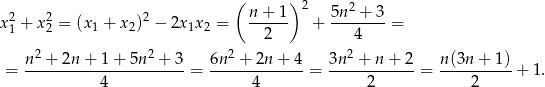
Musimy więc uzasadnić, że ułamek
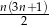 jest zawsze liczbą całkowitą. Nie jest to trudne: jeżeli
jest zawsze liczbą całkowitą. Nie jest to trudne: jeżeli  jest liczbą parzystą, to
jest liczbą parzystą, to 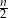 jest liczbą całkowitą i iloczyn
jest liczbą całkowitą i iloczyn 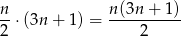
jest całkowity. Jeżeli natomiast
 jest liczbą nieparzystą, to parzysta jest liczba
jest liczbą nieparzystą, to parzysta jest liczba 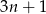 , czyli całkowita jest liczba
, czyli całkowita jest liczba 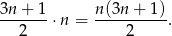
Powyższe uzasadnienie mogliśmy też zapisać następująco: jeżeli
 jest parzyste, to
jest parzyste, to 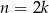 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 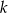 . Wtedy
. Wtedy 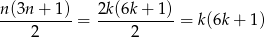
jest liczbą całkowitą. A jeżeli
 jest liczbą nieparzystą, tzn.
jest liczbą nieparzystą, tzn. 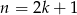 to
to 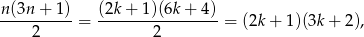
i ponownie jest to liczba całkowita.

