Zadanie nr 2421522
Wyznacz wszystkie liczby 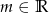 , dla których równanie
, dla których równanie 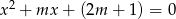 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 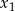 i
i 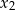 takie, że
takie, że 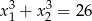 .
.
Rozwiązanie
Sprawdźmy najpierw kiedy równanie ma dwa różne pierwiastki
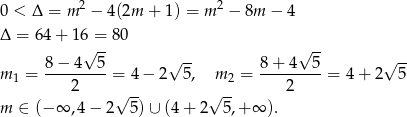
Korzystamy teraz ze wzorów Viète’a
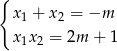
Musimy więc rozwiązać równanie.
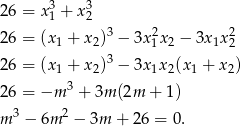
Szukamy pierwiastków wymiernych – sprawdzamy dzielniki wyrazu wolnego. Łatwo sprawdzić, że jednym z pierwiastków jest 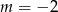 . Dzielimy wielomian przez
. Dzielimy wielomian przez 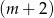 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
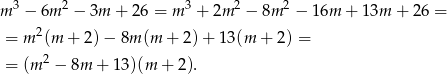
Rozkładamy teraz trójmian w pierwszym nawiasie
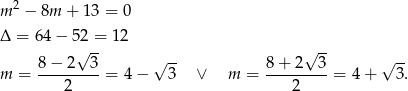
Ponieważ 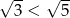 dwa powyższe rozwiązania nie znajdują się w zbiorze
dwa powyższe rozwiązania nie znajdują się w zbiorze 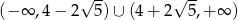 (czyli nie spełniają warunku z
(czyli nie spełniają warunku z 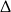 -ą). Łatwo sprawdzić, że
-ą). Łatwo sprawdzić, że 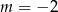 jest w przedziale
jest w przedziale 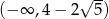 .
.
Odpowiedź: