/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 2957119

Dodaj do ulubionych
Dodaj do rozwiązanych

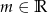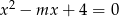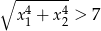Wyznacz wszystkie wartości m ∈ R , dla których równanie 2 x − mx + 4 = 0 ma dwa różne pierwiastki spełniające nierówność ∘ -------- x4+ x4 > 7 1 2 .

Rozwiązanie

Ponieważ 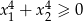4 4 x1 + x2 ≥ 0 , więc dana nierówność jest równoważna nierówności:

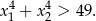
4 4 x 1 + x 2 > 49.

Sprawdźmy najpierw kiedy dane równanie ma dwa pierwiastki rzeczywiste.

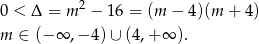
2 0 < Δ = m − 16 = (m − 4)(m + 4) m ∈ (− ∞ ,− 4)∪ (4,+ ∞ ).

Teraz korzystamy ze wzorów Viète’a

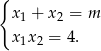
{ x + x = m 1 2 x1x2 = 4.

Musimy więc rozwiązać nierówność

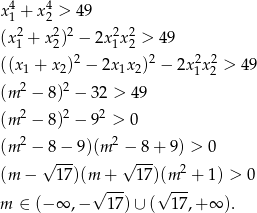
4 4 x 1 + x 2 > 49 (x 21 + x 22)2 − 2x 21x22 > 49 2 2 2 2 ((x 1 + x 2) − 2x 1x2) − 2x1x2 > 49 (m 2 − 8)2 − 32 > 49 (m 2 − 8)2 − 92 > 0 2 2 (m −√8-−-9)(m −√ -8+ 9) > 0 (m − 17)(m + 17)(m 2 + 1) > 0 √ --- √ --- m ∈ (− ∞ ,− 17) ∪ ( 17,+ ∞ ).

Zauważmy, że liczby 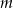m spełniające ten warunek spełniają też warunek Δ > 0 .  
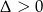Odpowiedź: √ --- √ --- m ∈ (− ∞ ,− 17)∪ ( 1 7,+ ∞ )

Wersja PDF