/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 3012018

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 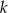k , dla których równanie

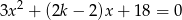
2 3x + (2k− 2)x+ 18 = 0

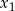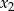ma dwa różne rozwiązania rzeczywiste x 1 i x 2 , przy czym 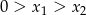0 > x 1 > x2 , spełniające warunek

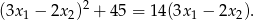
(3x 1 − 2x2)2 + 45 = 14(3x 1 − 2x2).

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa różne rozwiązania rzeczywiste.

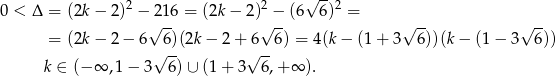
2 2 √ -- 2 0 < Δ = (2k − 2) − √216 = (2k − 2 )√ −-(6 6 ) = √ -- √ -- = (2k − 2 − 6 6)(2k − 2 + 6 6) = 4(k− (1+ 3 6))(k− (1− 3 6)) √ -- √ -- k ∈ (− ∞ ,1− 3 6)∪ (1 + 3 6 ,+∞ ).

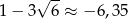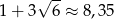Odnotujmy jeszcze, że √ -- 1 − 3 6 ≈ −6 ,35 i √ -- 1+ 3 6 ≈ 8,35 .

Spróbujmy teraz rozszyfrować warunek jaki mają spełniać pierwiastki równania. Jeżeli oznaczymy 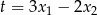t = 3x 1 − 2x 2 , to warunek ten przyjmuje postać.

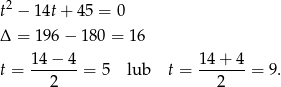
t2 − 14t + 45 = 0 Δ = 196− 180 = 16 14-−-4- 14-+-4- t = 2 = 5 lub t = 2 = 9 .

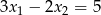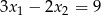Mamy zatem 3x1 − 2x2 = 5 lub 3x1 − 2x2 = 9 . Dodatkowo, na mocy wzorów Viète’a wiemy, że

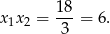
18- x 1x2 = 3 = 6.

Pierwiastki 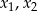x1,x2 spełniają więc jeden z układów równań

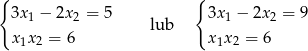
{ { 3x1 − 2x2 = 5 lub 3x 1 − 2x2 = 9 x1x2 = 6 x 1x2 = 6

Rozwiązujemy najpierw pierwszy układ – podstawiamy 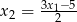x = 3x1−5 2 2 do drugiego równania.

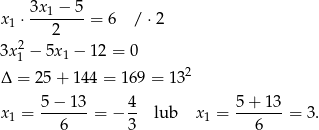
3x 1 − 5 x1 ⋅--------= 6 / ⋅2 2 2 3x 1 − 5x 1 − 1 2 = 0 Δ = 25 + 144 = 169 = 13 2 5−--13- 4- 5-+-13- x1 = 6 = − 3 lub x1 = 6 = 3.

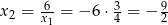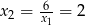Stąd x2 = 6x-= − 6⋅ 34 = − 92 1 i x2 = 6x-= 2 1 odpowiednio. Ponieważ rozwiązania mają być ujemne, drugą parę odrzucamy.

Podobnie rozwiązujemy drugi układ równań – podstawiamy 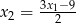3x1−9 x2 = 2 do drugiego równania.

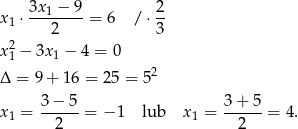
x1 ⋅ 3x1 −-9-= 6 / ⋅ 2 2 3 x21 − 3x1 − 4 = 0 2 Δ = 9 + 16 = 25 = 5 3 − 5 3 + 5 x1 = ------= − 1 lub x1 = ------= 4. 2 2

Drugie rozwiązanie odrzucamy (bo jest dodatnie) i mamy 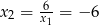x = -6 = − 6 2 x1 .

Dla obu otrzymanych par pierwiastków 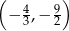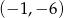( ) − 43,− 92 , (− 1,− 6) współczynnik 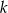k obliczamy ponownie stosując wzory Viète’a:

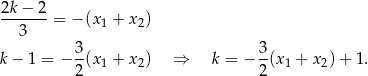
2k-−-2-= −(x 1 + x 2) 3 3- 3- k− 1 = − 2(x 1 + x 2) ⇒ k = − 2 (x1 + x 2)+ 1 .

Mamy zatem

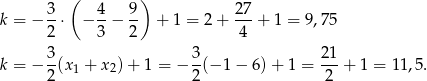
( ) k = − 3-⋅ − 4-− 9- + 1 = 2+ 27-+ 1 = 9 ,75 2 3 2 4 3 3 21 k = − --(x1 + x 2)+ 1 = − -(− 1 − 6) + 1 = ---+ 1 = 11 ,5 . 2 2 2

odpowiednio. Łatwo sprawdzić, że obie te wartości spełniają warunek z 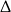Δ -ą.  
Odpowiedź: 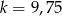k = 9 ,75 lub k = 11,5

Wersja PDF