/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 3405766

Dodaj do ulubionych
Dodaj do rozwiązanych

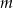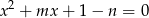Wykaż, że jeżeli m i n są takimi liczbami całkowitymi, że rozwiązania równania x 2 + mx + 1 − n = 0 są niezerowymi liczbami całkowitymi, to liczba 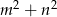m 2 + n2 nie jest liczbą pierwszą.

Rozwiązanie

Jeżeli oznaczmy przez 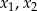x 1,x 2 rozwiązania danego równania, to mocy wzorów Viète’a mamy

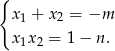
{ x1 + x2 = −m x x = 1 − n . 1 2

Mamy stąd

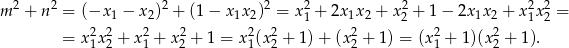
2 2 2 2 2 2 2 2 m + n = (−x 1 − x2) + (1− x1x2) = x1 + 2x1x 2 + x 2 + 1 − 2x 1x2 + x1x2 = = x21x22 + x21 + x22 + 1 = x 21(x22 + 1)+ (x22 + 1) = (x21 + 1)(x22 + 1).

Ponieważ z założenia 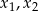x 1,x 2 są niezerowymi liczbami całkowitymi to powyższe wyrażenie jest iloczynem dwóch liczb całkowitych większych od 1. To oznacza, że 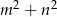m 2 + n2 jest liczbą złożoną.

Wersja PDF