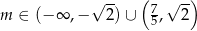Zadanie nr 4498984
Wyznacz wszystkie wartości parametru 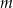 , dla których równanie
, dla których równanie 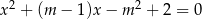 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 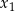 i
i 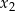
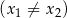 , spełniające warunek
, spełniające warunek 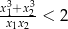 .
.
Rozwiązanie
Sprawdzamy najpierw, kiedy równanie ma dwa różne pierwiastki.
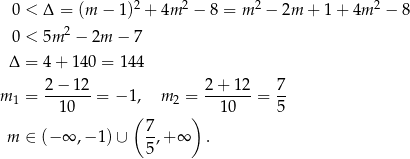
Przy tym założeniu możemy skorzystać ze wzorów Viète’a
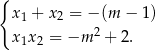
Zauważmy ponadto, że
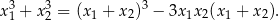
Mamy zatem do rozwiązania nierówność.
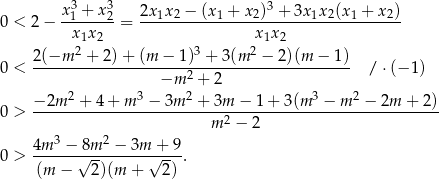
Szukamy teraz pierwiastków wymiernych wielomianu w liczniku – jednym z nich jest 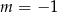 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 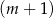 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
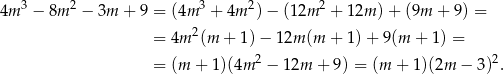
Mamy zatem nierówność
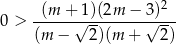
lub równoważnie
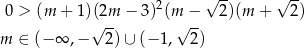
W połączeniu z warunkiem na 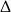 -ę mamy stąd
-ę mamy stąd
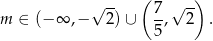
Odpowiedź: