Zadanie nr 4828049
Dla jakich wartości parametru 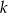 równanie
równanie 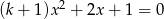 ma dwa rozwiązania przeciwnych znaków.
ma dwa rozwiązania przeciwnych znaków.
Rozwiązanie
Sposób I
Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki. Musi być kwadratowe, czyli 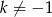 oraz
oraz
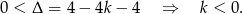
Pierwiastki będą przeciwnych znaków jeżeli ich iloczyn będzie ujemny. Ze wzorów Viète’a
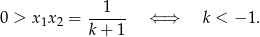
Mamy zatem
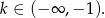
Sposób II
Zauważmy, że jeżeli 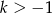 , to ramiona funkcji
, to ramiona funkcji 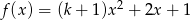 są skierowane w górę oraz
są skierowane w górę oraz 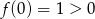 , więc w tym przypadku ewentualne pierwiastki
, więc w tym przypadku ewentualne pierwiastki 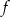 leżą po tej samej stronie osi
leżą po tej samej stronie osi 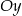 (czyli mają taki sam znak).
(czyli mają taki sam znak).
Jeżeli natomiast 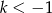 , to ramiona funkcji
, to ramiona funkcji 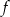 są skierowane w dół oraz
są skierowane w dół oraz 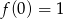 , więc w tym przypadku funkcja na pewno ma dwa pierwiastki i muszą one leżeć pod dwóch stronach osi
, więc w tym przypadku funkcja na pewno ma dwa pierwiastki i muszą one leżeć pod dwóch stronach osi 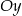 (czyli mają różne znaki).
(czyli mają różne znaki).
Dla 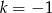 równanie jest liniowe, więc nie może mieć dwóch pierwiastków.
równanie jest liniowe, więc nie może mieć dwóch pierwiastków.
Odpowiedź: