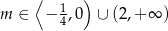Zadanie nr 4834311
Wyznacz wszystkie wartości parametru 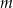 , dla których równanie
, dla których równanie
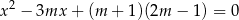
ma dwa różne rozwiązania 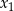 ,
, 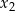 spełniające warunki:
spełniające warunki: 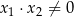 oraz
oraz 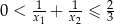 .
.
Rozwiązanie
Najpierw sprawdźmy, kiedy równanie ma dwa różne rozwiązania
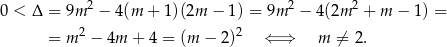
Rozwiązania mają być ponadto niezerowe, więc

Przy tych założeniach możemy zapisać wzory Viète’a.
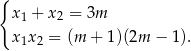
Rozwiązaniem nierówności
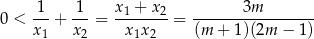
jest zbiór
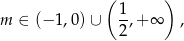
więc pozostało rozwiązać nierówność
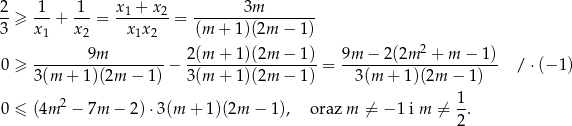
Rozkładamy teraz trójmian w pierwszym nawiasie.
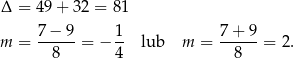
Mamy zatem nierówność
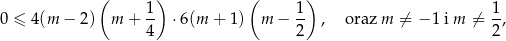
której rozwiązaniem jest zbiór
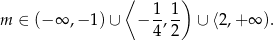
Łącząc wszystkie otrzymane warunki mamy
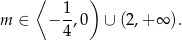
Odpowiedź: