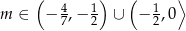Zadanie nr 4896139

Wyznacz wszystkie wartości parametru 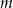, dla których funkcja kwadratowa 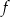określona wzorem

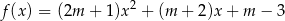
f (x) = (2m + 1)x2 + (m + 2)x+ m − 3

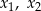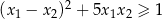ma dwa różne pierwiastki rzeczywiste x1, x 2 spełniające warunek (x1 − x2)2 + 5x 1x 2 ≥ 1 .

Rozwiązanie

Jeżeli funkcja 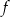ma być kwadratowa, to oczywiście musi być 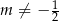1 m ⁄= − 2 . Sprawdźmy teraz, kiedy 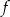ma dwa różne pierwiastki rzeczywiste.

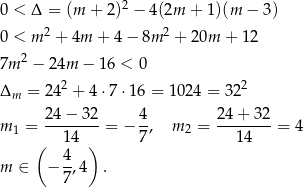
2 0 < Δ = (m + 2) − 4(2m + 1)(m − 3) 0 < m 2 + 4m + 4− 8m 2 + 2 0m + 12 7m 2 − 24m − 16 < 0 2 2 Δm = 24 + 4 ⋅7 ⋅16 = 10 24 = 32 24-−-32- 4- 24-+-32- m 1 = 14 = − 7 , m 2 = 14 = 4 ( 4 ) m ∈ − -,4 . 7

Jeżeli równanie ma pierwiastki to możemy zapisać wzory Viète’a

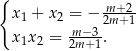
{ x1 + x2 = − m2m++21- x x = m-−3-. 1 2 2m+1

Przekształćmy teraz warunek z treści zadania tak, aby móc zastosować wzory Viète’a.

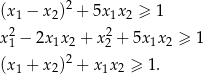
2 (x1 − x2) + 5x1x2 ≥ 1 x2 − 2x x + x2 + 5x x ≥ 1 1 1 2 2 1 2 (x1 + x2)2 + x1x2 ≥ 1.

Podstawiamy teraz ze wzorów Viète’a.

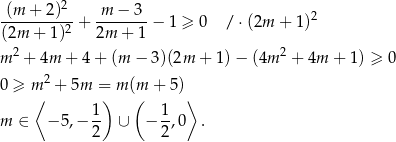
(m--+-2)2- -m-−-3- 2 (2m + 1)2 + 2m + 1 − 1 ≥ 0 / ⋅(2m + 1 ) 2 2 m + 4m + 4 + (m − 3)(2m + 1 )− (4m + 4m + 1) ≥ 0 0 ≥ m 2 + 5m = m (m + 5) ⟨ ) ( ⟩ 1- 1- m ∈ − 5,− 2 ∪ − 2,0 .

Łącząc wszystkie otrzymane warunki otrzymujemy

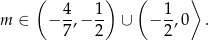
( ) ( ⟩ 4- 1- 1- m ∈ − 7 ,− 2 ∪ − 2 ,0 .

Odpowiedź: ( 4 1) ( 1 ⟩ m ∈ − 7 ,− 2 ∪ − 2,0