Zadanie nr 5022755
Liczby 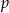 i
i 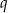 są pierwiastkami równania
są pierwiastkami równania 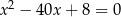 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 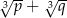 jest liczbą naturalną.
jest liczbą naturalną.
Rozwiązanie
Na mocy wzorów Viète’a wiemy, że jeżeli 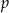 i
i 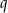 są pierwiastkami danego równania to
są pierwiastkami danego równania to
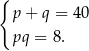
To w szczególności oznacza, że 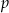 i
i 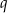 są liczbami dodatnimi. Jeżeli oznaczymy
są liczbami dodatnimi. Jeżeli oznaczymy 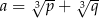 , to mamy
, to mamy
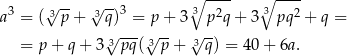
Liczba  jest więc dodatnim pierwiastkiem równania
jest więc dodatnim pierwiastkiem równania
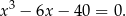
Szukamy wymiernych pierwiastków tego równania wśród dzielników wyrazu wolnego. Gdy to zrobimy, okaże się, że pierwiastkiem jest 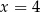 . Musimy jeszcze sprawdzić, czy nie ma innych pierwiastków – dzielimy lewą stronę przez
. Musimy jeszcze sprawdzić, czy nie ma innych pierwiastków – dzielimy lewą stronę przez 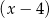 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
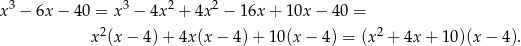
Trójmian w pierwszym nawiasie nie ma pierwiastków rzeczywistych (bo 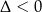 ), więc
), więc 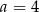 jest jedynym pierwiastkiem wielomianu
jest jedynym pierwiastkiem wielomianu 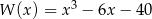 . W takim razie
. W takim razie