Zadanie nr 5234525
Wyznacz wszystkie wartości parametru 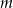 , dla których równanie
, dla których równanie 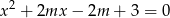 ma dwa różne pierwiastki należące do przedziału
ma dwa różne pierwiastki należące do przedziału 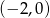 .
.
Rozwiązanie
Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki.
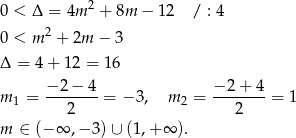
Zastanówmy się teraz jak zapisać informację o tym, że oba pierwiastki są w przedziale 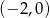 . Na pewno wierzchołek paraboli musi być w tym przedziale (bo znajduje się w środku między pierwiastkami). Zatem
. Na pewno wierzchołek paraboli musi być w tym przedziale (bo znajduje się w środku między pierwiastkami). Zatem
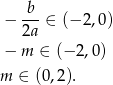
W połączeniu z warunkiem na 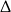 -ę daje to
-ę daje to 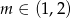 .
.
To jednak nie koniec, bo nawet jak wierzchołek jest w przedziale 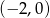 to pierwiastki mogą być na zewnątrz tego przedziału. Aby tak nie było, wartości funkcji w końcach przedziału muszą być dodatnie – wiemy już, że wartość w wierzchołku jest ujemna (warunek z
to pierwiastki mogą być na zewnątrz tego przedziału. Aby tak nie było, wartości funkcji w końcach przedziału muszą być dodatnie – wiemy już, że wartość w wierzchołku jest ujemna (warunek z 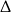 -ą), więc w takiej sytuacji pierwiastki będą musiały być w przedziale
-ą), więc w takiej sytuacji pierwiastki będą musiały być w przedziale 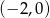 .
.
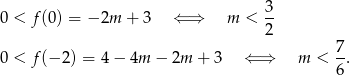
Zatem 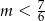 , co w połączeniu z wcześniej otrzymanym warunkiem daje
, co w połączeniu z wcześniej otrzymanym warunkiem daje 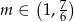 .
.
Odpowiedź: