/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 5338490

Dodaj do ulubionych
Dodaj do rozwiązanych

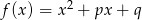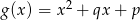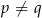Wykaż, że jeżeli funkcje 2 f(x ) = x + px + q i 2 g(x ) = x + qx + p , gdzie p ⁄= q , mają wspólne miejsce zerowe, to p + q = − 1 .

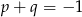Rozwiązanie

Jeżeli podane funkcje mają wspólne miejsce zerowe, to układ równań

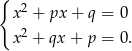
{ 2 x + px + q = 0 x2 + qx+ p = 0.

ma rozwiązanie. Odejmijmy od pierwszego równania drugie (żeby skrócić 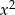2 x ).

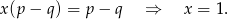
x (p− q) = p − q ⇒ x = 1.

Oczywiście skorzystaliśmy z założenia, że 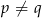p ⁄= q . Wstawiając 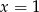x = 1 do któregokolwiek z równań, mamy

1 + p + q = 0 ⇒ p + q = − 1.
Wersja PDF