/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 5554564

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakiej wartości parametru 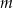m dwa różne pierwiastki 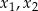x1,x2 równania

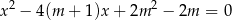
2 2 x − 4(m + 1)x + 2m − 2m = 0

spełniają warunek 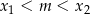x1 < m < x 2 .

Rozwiązanie

Sposób I

Wykresem lewej strony równania jest parabola 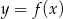y = f (x) o ramionach skierowanych w górę, więc warunek 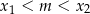x1 < m < x 2 jest równoważny nierówności

f(m ) < 0.

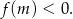
Rzeczywiście, jeżeli spełniony jest taki warunek, to parabola ta automatycznie przecina oś 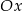Ox w punktach, które są położone po dwóch stronach punktu 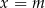x = m . Pozostało więc rozwiązać tę nierówność.

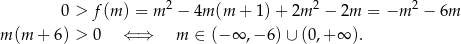
2 2 2 0 > f(m ) = m − 4m (m + 1 )+ 2m − 2m = −m − 6m m (m + 6) > 0 ⇐ ⇒ m ∈ (− ∞ ,− 6)∪ (0,+ ∞ ).

Sposób II

Sprawdzamy, kiedy dane równanie ma dwa pierwiastki.

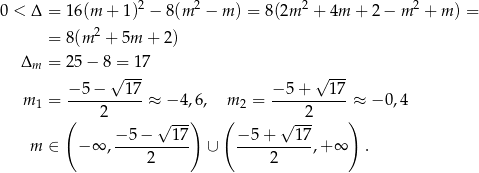
2 2 2 2 0 < Δ = 16(m + 1) − 8(m − m) = 8 (2m + 4m + 2 − m + m) = = 8(m 2 + 5m + 2) Δm = 25 − 8√=-1-7 √ --- − 5 − 17 − 5 + 17 m 1 = -----------≈ − 4,6, m 2 = -----------≈ − 0,4 ( 2 √ --) ( √ -2- ) −-5−----17- −-5+----17- m ∈ − ∞ , 2 ∪ 2 ,+ ∞ .

Pozostało rozwiązać nierówności

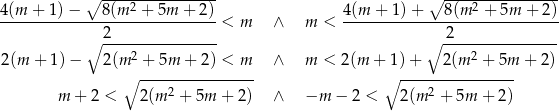
∘ ---------------- ∘ ---------------- 4(m + 1)− 8(m 2 + 5m + 2) 4(m + 1) + 8(m 2 + 5m + 2) --------------2--------------- < m ∧ m < ---------------2-------------- ∘ ---------------- ∘ ---------------- 2(m + 1) − 2(m 2 + 5m + 2) < m ∧ m < 2(m + 1)+ 2(m 2 + 5m + 2) ∘ ---------------- ∘ ---------------- m + 2 < 2(m 2 + 5m + 2) ∧ −m − 2 < 2(m 2 + 5m + 2)

Otrzymane nierówności są równoważne jednej nierówności

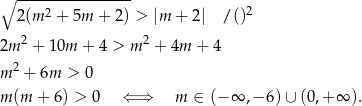
∘ ---------------- 2 (m 2 + 5m + 2) > |m + 2| /()2 2m 2 + 10m + 4 > m 2 + 4m + 4 2 m + 6m > 0 m (m + 6 ) > 0 ⇐ ⇒ m ∈ (− ∞ ,− 6)∪ (0,+ ∞ ).

Zauważmy jeszcze, że przy tym warunku, warunek z 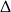Δ –ą jest spełniony automatycznie.  
Odpowiedź: m ∈ (− ∞ ,− 6)∪ (0,+ ∞ )

Wersja PDF