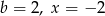/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 5711380

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że funkcja kwadratowa 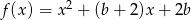2 f(x) = x + (b + 2)x + 2b , ma co najmniej jedno miejsce zerowe dla każdej wartości parametru 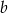b . Dla jakiej wartości parametru 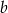b funkcja ma tylko jedno miejsce zerowe? Wyznacz to miejsce.

Rozwiązanie

Liczymy 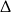Δ -ę.

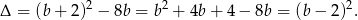
2 2 2 Δ = (b + 2) − 8b = b + 4b + 4 − 8b = (b− 2) .

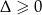Widać, że Δ ≥ 0 , czyli równanie ma zawsze rozwiązanie.

Rozwiązanie jest jedno gdy 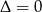Δ = 0 , czyli dla 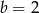b = 2 . Mamy wtedy równanie

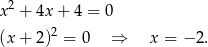
x2 + 4x+ 4 = 0 2 (x+ 2) = 0 ⇒ x = − 2.

 
Odpowiedź: b = 2 , x = −2

Wersja PDF