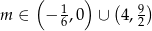/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 5713231

Dodaj do ulubionych
Dodaj do rozwiązanych

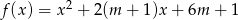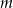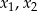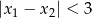Dany jest trójmian kwadratowy 2 f(x) = x + 2(m + 1)x + 6m + 1 . Wyznacz wszystkie rzeczywiste wartości parametru m , dla których ten trójmian ma dwa różne pierwiastki x1,x2 tego samego znaku, spełniające warunek |x − x | < 3 1 2 .

Rozwiązanie

Sprawdźmy najpierw kiedy dany trójmian ma dwa różne pierwiastki.

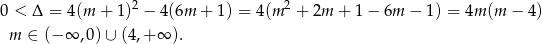
2 2 0 < Δ = 4(m + 1) − 4(6m + 1) = 4(m + 2m + 1 − 6m − 1) = 4m (m − 4) m ∈ (− ∞ ,0)∪ (4,+ ∞ ).

Przy tym założeniu możemy zapisać wzory Viète’a

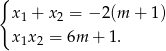
{ x 1 + x 2 = − 2(m + 1) x 1x 2 = 6m + 1.

Pierwiastki mają mieć ten sam znak, więc musi być spełniona nierówność

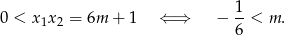
1- 0 < x1x2 = 6m + 1 ⇐ ⇒ − 6 < m .

Pozostało teraz rozwiązać nierówność

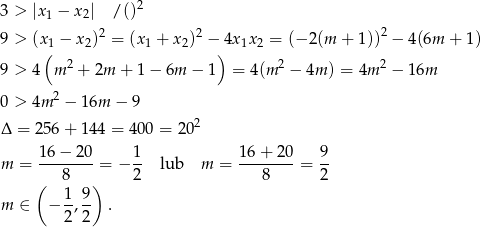
2 3 > |x1 − x2| / () 9 > (x 1 − x 2)2 = (x1 + x2)2 − 4x1x2 = (− 2(m + 1))2 − 4(6m + 1) ( ) 9 > 4 m 2 + 2m + 1− 6m − 1 = 4(m 2 − 4m ) = 4m 2 − 16m 0 > 4m 2 − 16m − 9 2 Δ = 256 + 144 = 400 = 20 16-−-2-0 1- 16+--20- 9- m = 8 = − 2 lub m = 8 = 2 ( 1 9 ) m ∈ − -,-- . 2 2

Łącząc wszystkie otrzymane warunki mamy

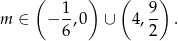
( ) ( ) 1- 9- m ∈ − 6 ,0 ∪ 4,2 .

 
Odpowiedź: ( 1 ) ( 9) m ∈ − 6,0 ∪ 4,2

Wersja PDF