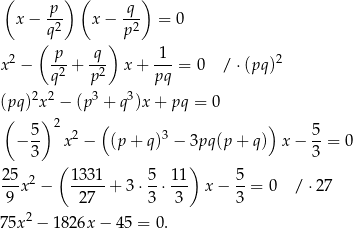Zadanie nr 5904214
Liczby 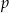 i
i 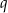 są pierwiastkami równania
są pierwiastkami równania 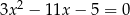 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 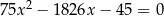 są liczby
są liczby 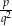 i
i 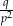 .
.
Rozwiązanie
Na mocy wzorów Viète’a liczby 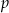 i
i 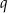 spełniają warunki
spełniają warunki
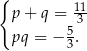
Liczby 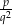 i
i 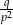 są pierwiastkami równania
są pierwiastkami równania
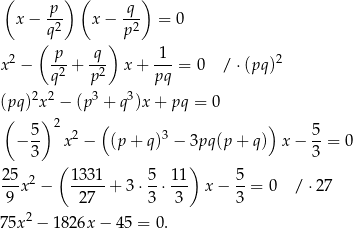
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Liczby 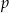 i
i 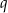 są pierwiastkami równania
są pierwiastkami równania 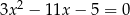 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 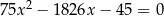 są liczby
są liczby 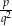 i
i 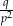 .
.
Na mocy wzorów Viète’a liczby 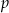 i
i 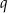 spełniają warunki
spełniają warunki
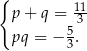
Liczby 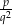 i
i 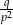 są pierwiastkami równania
są pierwiastkami równania