/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 5941030

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 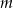m jeden pierwiastek równania 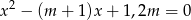x 2 − (m + 1)x + 1,2m = 0 jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?

Rozwiązanie

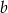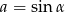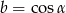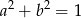Dwie liczby rzeczywiste a i b są postaci a = sin α i b = cosα dla pewnego α , wtedy i tylko wtedy gdy a2 + b2 = 1 (jedynka trygonometryczna). W treści mamy jednak dodatkowe żądanie, żeby kąt był ostry.

Na początek sprawdźmy kiedy 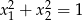x2+ x2 = 1 1 2 . Na mocy wzorów Viète’a mamy

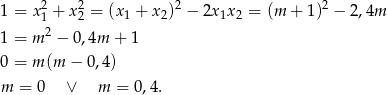
1 = x2 + x2 = (x + x )2 − 2x x = (m + 1 )2 − 2,4m 1 2 1 2 1 2 1 = m 2 − 0 ,4m + 1 0 = m (m − 0,4 ) m = 0 ∨ m = 0,4.

Dla 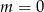m = 0 mamy równanie

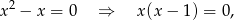
x2 − x = 0 ⇒ x(x − 1) = 0,

którego ma rozwiązania 0 i 1. Liczby te dopowiadają odpowiednio sinusowi i cosinusowi kąta 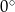0∘ , który nie jest kątem ostrym.

Jeżeli 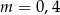m = 0,4 to mamy równanie

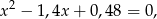
2 x − 1,4x + 0 ,48 = 0,

którego pierwiastkami są liczby 0,6 i 0,8 (liczymy z 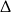Δ -y). Zatem wszystko gra.  
Odpowiedź: m = 0,4

Wersja PDF