Zadanie nr 6155610
Liczby 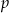 i
i 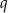 są pierwiastkami równania
są pierwiastkami równania 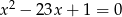 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 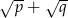 jest liczbą naturalną.
jest liczbą naturalną.
Rozwiązanie
Na mocy wzorów Viète’a wiemy, że jeżeli 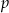 i
i 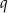 są pierwiastkami danego równania to
są pierwiastkami danego równania to
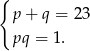
To w szczególności oznacza, że 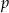 i
i 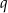 są liczbami dodatnimi. Jeżeli oznaczymy
są liczbami dodatnimi. Jeżeli oznaczymy 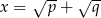 , to mamy
, to mamy
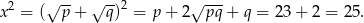
W takim razie 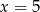 .
.

