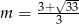Zadanie nr 6468003
Wyznacz wszystkie wartości parametru 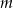 , dla których jedno rozwiązanie równania
, dla których jedno rozwiązanie równania
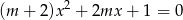
jest sinusem, a drugie cosinusem tego samego kąta?
Rozwiązanie
Jeżeli równanie ma mieć dwa rozwiązania to musi kwadratowe, czyli musi być 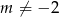 .
.
Dwie liczby rzeczywiste  i
i 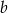 są postaci
są postaci 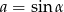 i
i 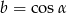 dla pewnego
dla pewnego  , wtedy i tylko wtedy gdy
, wtedy i tylko wtedy gdy 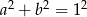 (jedynka trygonometryczna).
(jedynka trygonometryczna).
Aby sprawdzić, kiedy pierwiastki podanego równania spełniają taki warunek, korzystamy ze wzorów Viète’a.
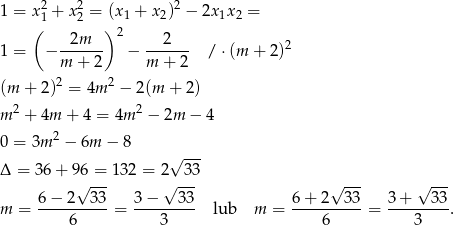
To jeszcze nie koniec, bo musimy sprawdzić, czy dla tych wartości 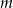 równanie rzeczywiście ma dwa pierwiastki. Rozwiązujemy nierówność:
równanie rzeczywiście ma dwa pierwiastki. Rozwiązujemy nierówność:
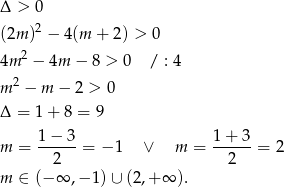
Ponieważ 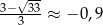 i
i 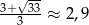 tylko dla drugiej z tych liczb równanie ma dwa rozwiązania.
tylko dla drugiej z tych liczb równanie ma dwa rozwiązania.
Odpowiedź: