Zadanie nr 6523824
Suma współczynników 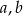 i
i  równania
równania 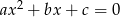 wynosi 24. Różnice
wynosi 24. Różnice 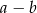 i
i 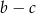 są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
Rozwiązanie
Jeżeli 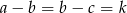 , to mamy
, to mamy
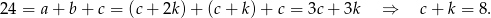
Wiemy ponadto, że -3 jest rozwiązaniem równania, czyli
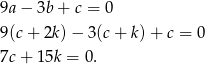
Mamy więc układ równań
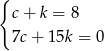
Stąd
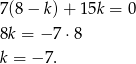
Zatem 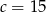 ,
, 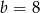 i
i 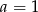 . Teraz ze wzorów Viète’a mamy
. Teraz ze wzorów Viète’a mamy
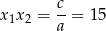
czyli drugi pierwiastek to 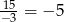 .
.
Odpowiedź: -5

