Zadanie nr 7071933
Dla jakich wartości parametru 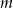 suma kwadratów dwóch różnych pierwiastków równania
suma kwadratów dwóch różnych pierwiastków równania 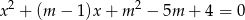 przyjmuje wartość największą. Wyznacz tę wartość.
przyjmuje wartość największą. Wyznacz tę wartość.
Rozwiązanie
Na początku sprawdźmy kiedy równanie ma dwa pierwiastki.
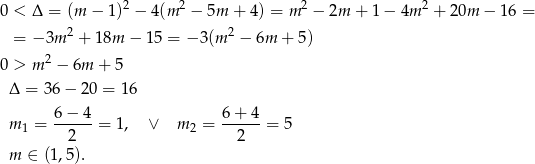
Na mocy wzorów Viete’a mamy
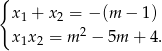
Zatem
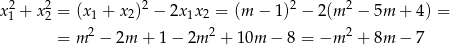
Wykresem tego wyrażenia jest parabola o ramionach skierowanych w dół, a jego dziedziną zbiór 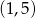 . Ponieważ pierwsza współrzędna wierzchołka tej paraboli
. Ponieważ pierwsza współrzędna wierzchołka tej paraboli 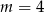 znajduje się w tym przedziale, to właśnie w nim powyższe wyrażenie przyjmuje największą wartość, która jest równa
znajduje się w tym przedziale, to właśnie w nim powyższe wyrażenie przyjmuje największą wartość, która jest równa
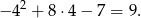
Odpowiedź: 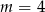 , największa wartość: 9.
, największa wartość: 9.

