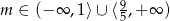/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 7444001

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 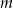m , dla których równanie

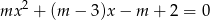
2 mx + (m − 3)x − m + 2 = 0

ma co najmniej jedno dodatnie rozwiązanie.

Rozwiązanie

Jeżeli 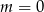m = 0 to mamy równanie 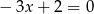− 3x + 2 = 0 , które ma rozwiązanie dodatnie.

Jeżeli równanie jest kwadratowe, to sprawdźmy kiedy ma rozwiązania

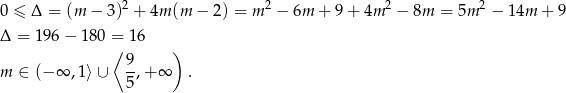
0 ≤ Δ = (m − 3 )2 + 4m (m − 2) = m 2 − 6m + 9+ 4m 2 − 8m = 5m 2 − 14m + 9 Δ = 196− 180 = 1 6 ⟨ ) 9- m ∈ (−∞ ,1 ⟩∪ 5,+ ∞ .

Zamiast sprawdzać kiedy co najmniej jeden z pierwiastków jest dodatni, łatwiej jest sprawdzić kiedy oba są niedodatnie. Pierwiastki są niedodatnie jeżeli ich suma jest niedodatnia, a iloczyn nieujemny. Na mocy wzorów Viète’a mamy

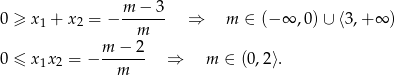
m-−-3- 0 ≥ x1 + x2 = − m ⇒ m ∈ (−∞ ,0 )∪ ⟨3,+ ∞ ) m − 2 0 ≤ x1x 2 = − ------ ⇒ m ∈ (0,2⟩. m

Ponieważ te warunki są ze sobą sprzeczne, co najmniej jeden z pierwiastków jest zawsze dodatni.  
Odpowiedź: m ∈ (− ∞ ,1⟩∪ ⟨ 95,+ ∞ )

Wersja PDF