/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 7617508

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź tę wartość parametru 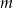m , dla której iloczyn pierwiastków równania 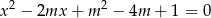x 2 − 2mx + m 2 − 4m + 1 = 0 jest najmniejszy.

Rozwiązanie

Zadanie rozwiążemy korzystając ze wzorów Viète’a, ale zanim to zrobimy, sprawdźmy, kiedy równanie ma pierwiastki.

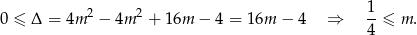
0 ≤ Δ = 4m 2 − 4m 2 + 16m − 4 = 16m − 4 ⇒ 1-≤ m . 4

Na mocy wzorów Viète’a iloczyn pierwiastków równania jest równy

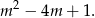
2 m − 4m + 1.

Wyrażenie to przyjmuje najmniejszą wartość w wierzchołku paraboli będącej jego wykresem, czyli dla

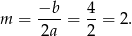
m = −b--= 4-= 2. 2a 2

 
Odpowiedź: m = 2

Wersja PDF