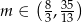Zadanie nr 8053787
Wyznacz wszystkie wartości parametru 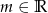 , dla których równanie
, dla których równanie 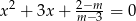 ma dwa różne pierwiastki
ma dwa różne pierwiastki 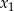 i
i 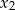 takie, że
takie, że 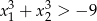 .
.
Rozwiązanie
Ze względu na 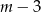 w mianowniku musi być
w mianowniku musi być 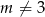 .
.
Sprawdzamy teraz, kiedy równanie ma dwa różne pierwiastki.
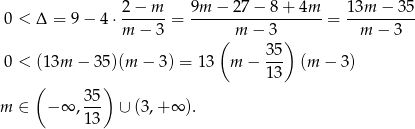
Przy tym założeniu możemy skorzystać ze wzorów Viète’a
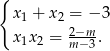
Zauważmy ponadto, że
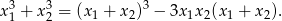
Mamy zatem do rozwiązania nierówność.
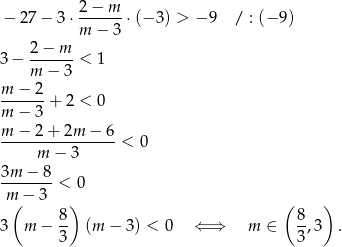
W połączeniu z warunkiem na  -ę mamy stąd
-ę mamy stąd
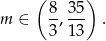
Odpowiedź: