/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 8081017

Dodaj do ulubionych
Dodaj do rozwiązanych

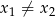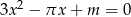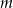Liczby x1 ⁄= x2 są dwoma dodatnimi pierwiastkami równania 2 3x − πx + m = 0 z niewiadomą x , gdzie m jest pewną ustaloną liczbą rzeczywistą.

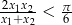  • Wykaż, że 2x1x2 < π- x1+x2 6 .
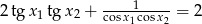  • Wykaż, że ----1----- 2tg x1tg x2 + cosx1cosx2 = 2 .

Rozwiązanie

Sprawdźmy kiedy dane równanie ma dwa różne pierwiastki

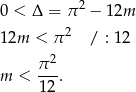
2 0 < Δ = π − 12m 12m < π 2 / : 12 2 m < π--. 12
  • Na mocy wzorów Viète’a mamy
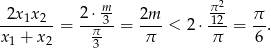
    2x1x 2 2 ⋅ m 2m π2- π --------= --π3-= --- < 2⋅ 12-= --. x1 + x2 3 π π 6
  • Przekształcamy równoważnie równość, którą mamy udowodnić.
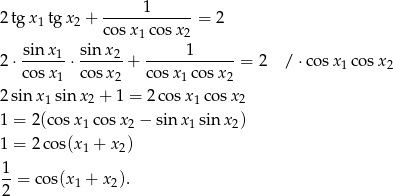
    1 2tg x1tg x2 + ------------ = 2 cosx 1cos x2 2⋅ sin-x1-⋅ sin-x2-+ -----1------= 2 / ⋅co sx cosx cosx 1 cosx2 cosx1 cosx 2 1 2 2sin x sinx + 1 = 2co sx co sx 1 2 1 2 1 = 2(cos x1co sx2 − sinx1 sin x2) 1 = 2 cos(x + x ) 1 2 1-= co s(x + x ). 2 1 2

    Otrzymany warunek jest oczywiście spełniony, bo na mocy wzorów Viète’a

    π x1 + x2 = 3-.
Wersja PDF