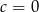Zadanie nr 8090614
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 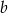 ,
,  równanie
równanie 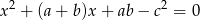 ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Rozwiązanie
Ponieważ mamy do czynienia z równaniem kwadratowym, o tym ile ma ono rozwiązań decyduje 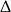 .
.
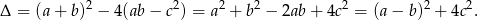
Widać więc, że zawsze 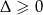 , czyli równanie ma zawsze rozwiązanie.
, czyli równanie ma zawsze rozwiązanie.
Aby równanie miało dokładnie jedno rozwiązanie, musi być 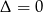 , czyli
, czyli 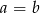 i
i 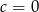 .
.
Odpowiedź: Jedno rozwiązanie jest dla 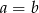 i
i