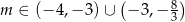Zadanie nr 8428848

Wyznacz wszystkie wartości parametru 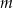, dla których równanie

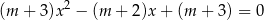
2 (m + 3)x − (m + 2)x + (m + 3) = 0

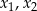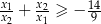ma dwa różne rozwiązania x1,x2 spełniające nierówność: x x 14 x12 + x21 ≥ − 9- .

Rozwiązanie

Równanie musi być oczywiście kwadratowe, więc 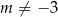m ⁄= − 3 . Ponadto musi być

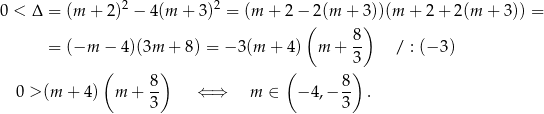
2 2 0 < Δ = (m + 2) − 4 (m + 3) = (m + 2 −(2(m + 3)))(m + 2 + 2 (m + 3)) = 8 = (−m − 4 )(3m + 8) = − 3(m + 4) m + -- / : (− 3 ) ( ) ( 3) 8- 8- 0 > (m + 4 ) m + 3 ⇐ ⇒ m ∈ − 4,− 3 .

Przy tym założeniu możemy zapisać wzory Viète’a

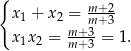
{ m+ 2 x 1 + x 2 = m+-3 x 1x2 = m-+3 = 1. m +3

Pozostało rozwiązać nierówność

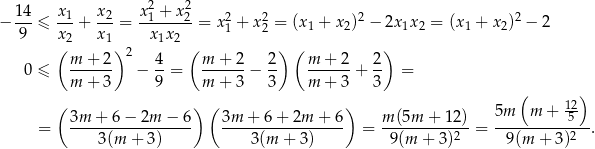
14 x x x2 + x2 − ---≤ -1-+ --2= -1----2-= x21 + x22 = (x1 + x2)2 − 2x1x 2 = (x1 + x2)2 − 2 9 x2 x 1 x1x2 ( m + 2 )2 4 ( m + 2 2) ( m + 2 2 ) 0 ≤ ------ − --= ------− -- ------ + -- = m + 3 9 m + 3 3 m + 3 3 ( ) ( ) ( ) 5m m + 12 = 3m-+-6-−-2m--−-6- 3m-+-6-+-2m--+-6- = m(5m--+-12)-= ----------5--. 3 (m + 3) 3 (m + 3) 9(m + 3)2 9(m + 3 )2

Rozwiązaniem tej nierówności jest zbiór

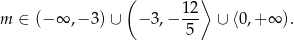
( ⟩ 12- m ∈ (− ∞ ,− 3) ∪ − 3,− 5 ∪ ⟨0,+ ∞ ).

Uwzględniając warunek z 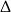–ą mamy zatem

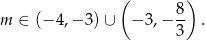
( ) 8 m ∈ (−4 ,−3 )∪ − 3,− 3- .

Odpowiedź: ( 8) m ∈ (− 4,− 3)∪ −3 ,− 3