/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 8685550

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 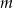m równanie 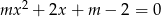2 mx + 2x + m − 2 = 0 ma dwa różne pierwiastki mniejsze od 1?

Rozwiązanie

Po pierwsze, jeżeli równanie ma mieć dwa różne pierwiastki, to musi być kwadratowe (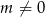m ⁄= 0 ) oraz Δ > 0 .

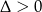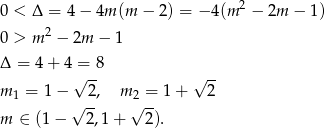
2 0 < Δ = 4− 4m (m − 2 ) = − 4(m − 2m − 1) 0 > m 2 − 2m − 1 Δ = 4+ 4 = 8 √ -- √ -- m 1 = 1− √ -2, m√2 =-1 + 2 m ∈ (1 − 2 ,1+ 2).

Sposób I

Jak zapisać warunek, że pierwiastki są mniejsze od 1? – najlepiej jest myśleć o paraboli, jej punkty przecięcia z osią 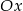Ox muszą być na lewo od 1.

PIC

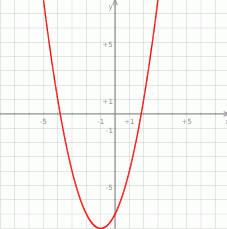
Jak to zapisać? Na pewno wierzchołek musi być na lewo od 1, czyli

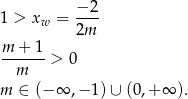
− 2 1 > xw = ---- 2m m--+-1 > 0 m m ∈ (− ∞ ,− 1)∪ (0,+ ∞ ).

To jednak nie wystarczy, bo większy pierwiastek może być nadal za jedynką. Aby to wykluczyć, musimy jeszcze zażądać aby wartość w 1 była dodatnia dla 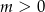m > 0 i ujemna dla 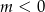m < 0 . Ponieważ jednak

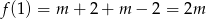
f(1) = m + 2 + m − 2 = 2m

warunek ten jest zawsze spełniony.

Sposób II

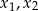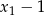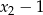Jeżeli pierwiastki x1,x2 danego równania mają być mniejsze od 1, to liczby x1 − 1 i x 2 − 1 muszą być obie ujemne. Tak jest wtedy i tylko wtedy, gdy ich iloczyn jest dodatni, a suma ujemna.

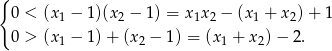
{ 0 < (x1 − 1)(x 2 − 1) = x1x2 − (x1 + x2)+ 1 0 > (x1 − 1) + (x2 − 1) = (x 1 + x 2)− 2.

Korzystamy teraz ze wzorów Viète’a.

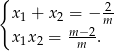
{ x1 + x2 = − -2 m−2-m x1x2 = m .

Musimy więc rozwiązać układ nierówności

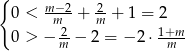
{ 0 < m-−m2 + m2+ 1 = 2 0 > − -2− 2 = − 2 ⋅ 1+m m m

Rozwiązaniem tego układu jest oczywiście zbiór 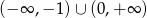(−∞ ,− 1) ∪ (0,+ ∞ ) . W połączeniu z warunkiem na 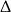Δ -ę mamy stąd √ -- m ∈ (0,1+ 2) .  
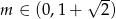Odpowiedź: m ∈ (0,1 + √ 2)

Wersja PDF