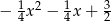Zadanie nr 8826955
Funkcja kwadratowa postaci 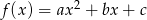 , posiada miejsca zerowe równe -3 i 2, a jej współczynnik
, posiada miejsca zerowe równe -3 i 2, a jej współczynnik 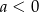 . Oblicz wartości współczynników
. Oblicz wartości współczynników 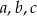 wiedząc, ze największa wartość funkcji wynosi
wiedząc, ze największa wartość funkcji wynosi 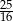 .
.
Rozwiązanie
Z podanych miejsc zerowych wiemy, że funkcja jest postaci
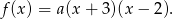
Ponieważ wierzchołek funkcji kwadratwej znajduje się dokładnie pomiędzy miejscami zerowymi, więc 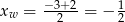 . Dokładnie w tym punkcie funkcja przyjmuje wartość największą (bo
. Dokładnie w tym punkcie funkcja przyjmuje wartość największą (bo 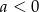 ), czyli
), czyli
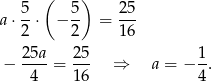
Zatem
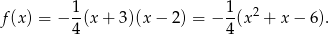
Na koniec, dla ciekawskich, wykres funkcji 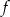 .
.
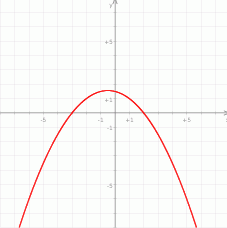
Odpowiedź: