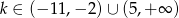/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 8912557

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości 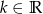k ∈ R równanie 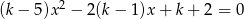2 (k− 5)x − 2(k − 1)x + k + 2 = 0 ma dwa różne pierwiastki dodatnie?

Rozwiązanie

Jeżeli równanie ma mieć dwa pierwiastki to musi być kwadratowe, czyli 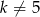k ⁄= 5 . Ponadto delta musi być dodatnia.

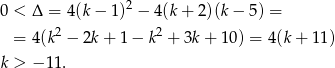
2 0 < Δ = 4(k − 1) − 4(k + 2)(k − 5) = = 4 (k2 − 2k + 1 − k2 + 3k + 10) = 4(k+ 11) k > − 11 .

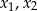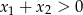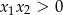Pierwiastki x1,x2 będą dodatnie jeżeli x1 + x2 > 0 i x1x 2 > 0 . Na mocy wzorów Viète’a otrzymujemy nierówności.

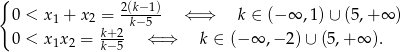
{ 0 < x1 + x 2 = 2(k−1) ⇐ ⇒ k ∈ (− ∞ ,1)∪ (5,+ ∞ ) k+-2k− 5 0 < x1x2 = k− 5 ⇐ ⇒ k ∈ (− ∞ ,− 2)∪ (5,+ ∞ ).

Uwzględniając warunek z 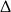Δ -ą otrzymujemy

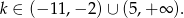
k ∈ (− 11 ,− 2 )∪ (5,+ ∞ ).

 
Odpowiedź: k ∈ (− 11,− 2) ∪ (5,+ ∞ )

Wersja PDF