Zadanie nr 9269203
Liczby 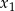 i
i 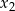 są pierwiastkami równania
są pierwiastkami równania 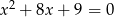 . Oblicz
. Oblicz 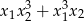 .
.
Rozwiązanie
Na mocy wzorów Viète’a wiemy, że jeżeli 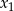 i
i 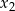 są pierwiastkami danego równania to
są pierwiastkami danego równania to
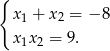
Musimy teraz przekształcić wyrażenie 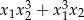 tak, aby wyrazić je w zależności od
tak, aby wyrazić je w zależności od 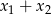 i
i 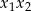 . Liczymy
. Liczymy
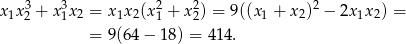
Odpowiedź: 414

