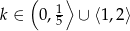/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 9531902

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 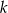k równanie 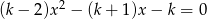2 (k − 2)x − (k + 1)x − k = 0 ma tylko ujemne rozwiązania?

Rozwiązanie

Jeżeli 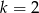k = 2 , to mamy równanie 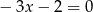− 3x − 2 = 0 , które ma ujemne rozwiązanie. Będziemy więc dalej zakładać, że mamy równanie kwadratowe.

Sprawdźmy kiedy równanie ma rozwiązania

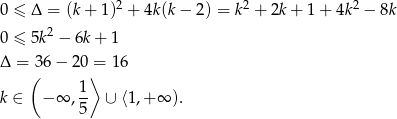
0 ≤ Δ = (k+ 1)2 + 4k(k− 2) = k2 + 2k + 1+ 4k2 − 8k 2 0 ≤ 5k − 6k + 1 Δ = 36− 20 = 16 ( ⟩ k ∈ − ∞ , 1 ∪ ⟨1 ,+ ∞ ). 5

Obydwa pierwiastki będą ujemne jeżeli ich suma jest ujemna a iloczyn dodatni, czyli na mocy wzorów Viète’a

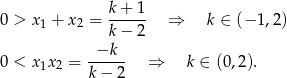
k-+-1- 0 > x1 + x2 = k − 2 ⇒ k ∈ (−1 ,2) −k 0 < x1x2 = ------ ⇒ k ∈ (0,2). k − 2

W połączeniu z wcześniej znalezionymi warunkami mamy

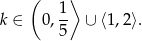
( 1 ⟩ k ∈ 0,-- ∪ ⟨1,2⟩. 5

 
Odpowiedź: ( ⟩ k ∈ 0, 15 ∪ ⟨1,2⟩

Wersja PDF