/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 9783035

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 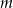m , dla których jeden z pierwiastków równania

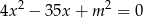
4x 2 − 35x + m2 = 0

jest kwadratem drugiego pierwiastka. Oblicz te pierwiastki.

Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa pierwiastki

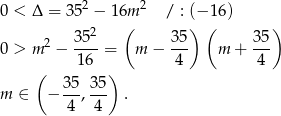
2 2 0 < Δ = 35 − 16(m / : ()− 1(6 ) ) 2 352 35 35 0 > m − 16--= m − 4-- m + -4- ( ) 35- 35- m ∈ − 4 ,4 .

Przy tym założeniu, na mocy wzorów Viète’a mamy

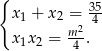
{ x1 + x2 = 35 m-2 4 x1x2 = 4 .

Wiemy ponadto, że 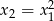x2 = x 21 , czyli

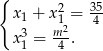
{ x1 + x21 = 354 3 m-2 x1 = 4 .

Rozwiążmy pierwsze równanie kwadratowe

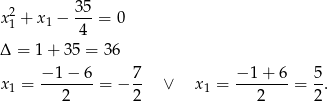
35 x21 + x1 − ---= 0 4 Δ = 1 + 35 = 36 − 1 − 6 7 − 1+ 6 5 x1 = ------- = − -- ∨ x1 = ------- = --. 2 2 2 2

Pierwsza możliwość daje

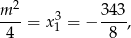
m 2 3 343 --- = x 1 = − ---, 4 8

co jest niemożliwe. Zatem 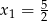x = 5 1 2 oraz

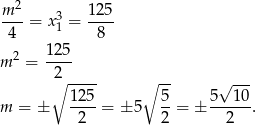
m 2 3 125 ---= x1 = ---- 4 8 m2 = 125- ∘2 ---- ∘ -- √ --- 125 5 5 10 m = ± ----= ± 5 --= ± ------. 2 2 2

Otrzymujemy wtedy równanie

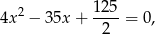
2 125 4x − 3 5x+ ----= 0, 2

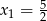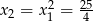którego pierwiastkami są x = 5 1 2 i x = x2 = 25- 2 1 4 .  
Odpowiedź: √ -- √ -- m = − 5-210-, lub m = 5-210,x 1 = 52,x2 = 245

Wersja PDF