/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 9871718

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 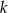k równanie 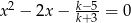2 k−5- x − 2x− k+3 = 0 ma dwa pierwiastki jednakowych znaków, których suma kwadratów jest nie mniejsza od 3?

Rozwiązanie

Oczywiście ze względu na mianownik musimy założyć, że 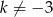k ⁄= − 3 .

Sprawdźmy najpierw kiedy podane równanie ma dwa pierwiastki.

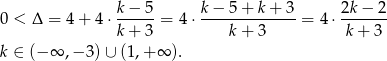
0 < Δ = 4+ 4 ⋅ k-−-5-= 4⋅ k−--5+--k+--3 = 4 ⋅ 2k-−-2 k + 3 k+ 3 k+ 3 k ∈ (− ∞ ,− 3) ∪ (1,+ ∞ ).

Skorzystamy teraz ze wzorów Viète’a.

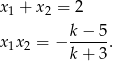
x1 + x2 = 2 x1x 2 = − k−--5. k+ 3

Pierwiastki będą jednakowych znaków jeżeli ich iloczyn jest dodatni, czyli

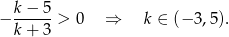
− k-−-5-> 0 ⇒ k ∈ (− 3,5). k + 3

Pozostało sprawdzić kiedy suma kwadratów jest nie mniejsza niż 3.

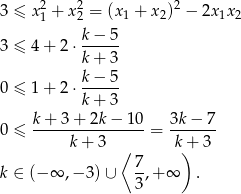
2 2 2 3 ≤ x1 + x2 = (x1 + x2) − 2x1x 2 k−-5-- 3 ≤ 4+ 2⋅ k+ 3 k− 5 0 ≤ 1+ 2⋅ ------ k+ 3 k+--3+--2k−--10- 3k−--7- 0 ≤ k+ 3 = k + 3 ⟨ ) k ∈ (− ∞ ,− 3) ∪ 7,+ ∞ . 3

Wszystkie trzy otrzymane nierówności dają nam łącznie 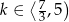⟨ ) k ∈ 73,5 .  
Odpowiedź: k ∈ ⟨7 ,5) 3

Wersja PDF