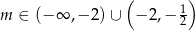/Szkoła średnia/Równania/Kwadratowe

Zadanie nr 9978901

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 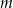m , dla których równanie 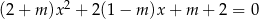(2 + m )x2 + 2(1 − m )x + m + 2 = 0 ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.

Rozwiązanie

Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki rzeczywiste. Oczywiście musi być 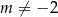m ⁄= −2 oraz

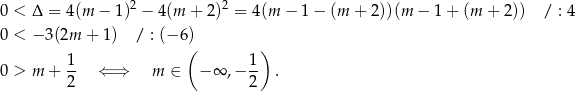
2 2 0 < Δ = 4(m − 1) − 4(m + 2) = 4(m − 1 − (m + 2))(m − 1+ (m + 2)) / : 4 0 < − 3(2m + 1) / : (− 6) ( ) 0 > m + 1- ⇐ ⇒ m ∈ − ∞ ,− 1- . 2 2

To oznacza, że dane równanie ma dwa pierwiastki dla

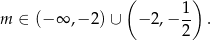
( 1 ) m ∈ (− ∞ ,− 2)∪ − 2,− -- . 2

Przy tym założeniu, na mocy wzorów Viète’a wiemy, że

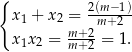
{ 2(m −1) x1 + x2 = -m+-2- x1x 2 = m+-2 = 1. m+ 2

Pozostało rozwiązać nierówność

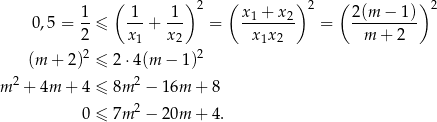
( ) 2 ( ) 2 ( ) 2 0,5 = 1-≤ -1-+ 1-- = x1-+-x2- = 2(m--−-1) 2 x 1 x2 x 1x2 m + 2 (m + 2)2 ≤ 2 ⋅4(m − 1)2 m 2 + 4m + 4 ≤ 8m 2 − 16m + 8 2 0 ≤ 7m − 20m + 4.

Rozwiązujemy otrzymaną nierówność kwadratową.

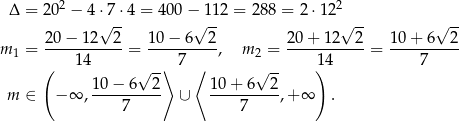
Δ = 20 2 − 4 ⋅7 ⋅4 = 400 − 1 12 = 288 = 2⋅12 2 √ -- √ -- √ -- √ -- 20−--12--2- 10−--6--2- 20-+-12--2- 10-+-6--2- m 1 = 14 = 7 , m2 = 14 = 7 ( √ --⟩ ⟨ √ -- ) m ∈ − ∞ , 10-−-6-2- ∪ 10-+-6--2-,+ ∞ . 7 7

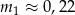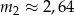Ponieważ m 1 ≈ 0,2 2 i m2 ≈ 2,64 , łącząc wszystkie warunki otrzymujemy

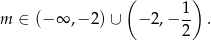
( ) m ∈ (− ∞ ,− 2)∪ − 2,− 1- . 2

 
Odpowiedź: ( ) m ∈ (− ∞ ,− 2)∪ − 2,− 1 2

Wersja PDF