/Szkoła średnia/Równania/Z wartością bezwględną/Układy równań/Liniowy

Zadanie nr 9898047

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 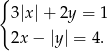{ 3|x |+ 2y = 1 2x− |y | = 4.

Rozwiązanie

Sposób I

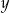Rozważmy osobno 4 przypadki różnych znaków x i y . Tak naprawdę, jak ktoś ma dobre oko, to z drugiego równania 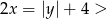2x = |y|+ 4 > , czyli 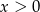x > 0 i mamy do rozpatrzenia tylko dwa przypadki. Gdybyśmy tego nie zobaczyli, to trzebaby dodatkowo rozważyć dwa przypadki – żadne nieszczęście, po prostu odrobina więcej rachunków.

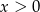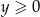Jeżeli x > 0 i y ≥ 0 to mamy układ

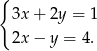
{ 3x + 2y = 1 2x − y = 4 .

Dodając do pierwszego równania 2 razy drugie (żeby skrócić 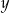y ) mamy

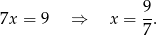
9 7x = 9 ⇒ x = 7.

Z drugiego równania mamy

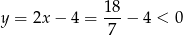
18- y = 2x − 4 = 7 − 4 < 0

Co jest sprzeczne z założeniem 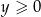y ≥ 0 .

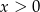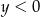Jeżeli x > 0 i y < 0 to mamy układ

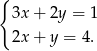
{ 3x + 2y = 1 2x + y = 4 .

Odejmując od pierwszego równania 2 razy drugie (żeby skrócić 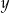y ) mamy

−x = − 7 ⇒ x = 7.

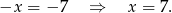
Z drugiego równania mamy

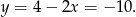
y = 4 − 2x = −1 0.

Sposób II

Zadanie możemy też rozwiązać graficznie. Pierwsze równanie 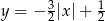3 1 y = − 2|x|+ 2 to proste

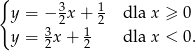
{ y = − 32x + 12 dla x ≥ 0 3 1 y = 2x + 2 dla x < 0.

Podobnie drugie 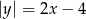|y| = 2x − 4 to proste

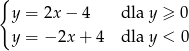
{ y = 2x − 4 dla y ≥ 0 y = − 2x + 4 dla y < 0

Jeżeli narysuje się te wykresy w miarę dokładnie, to można zauważyć, że przecinają się tylko w punkcie 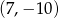(7 ,−1 0) .

PIC

 
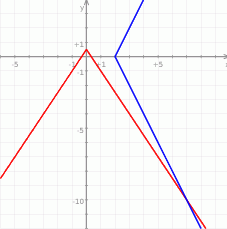
Odpowiedź: (x,y) = (7,− 10)

Wersja PDF